Уравнение Бернулли для установившегося движения идеальной жидкости
Уравнение Бернулли для элементарного потока идеальной жидкости устанавливает связь между скоростью движения, давлением и геометрическим положением частиц.
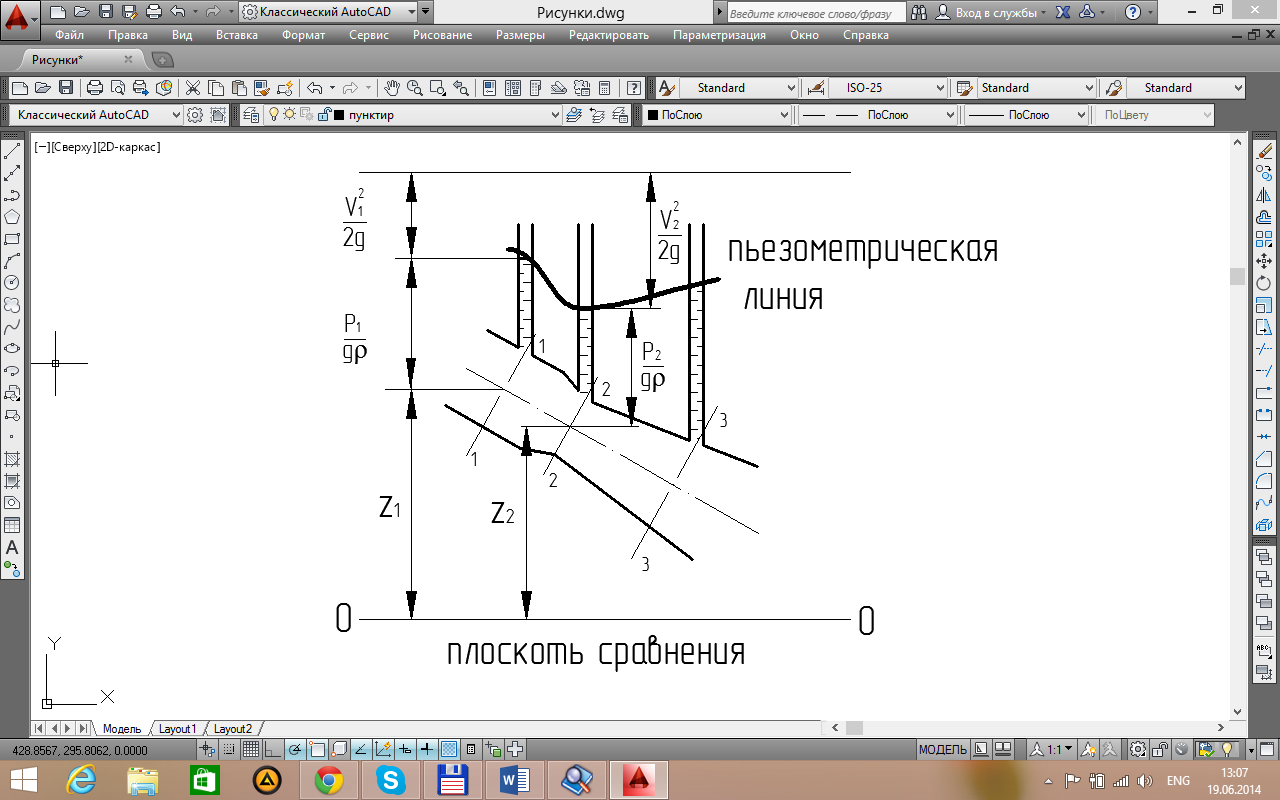
Рисунок 3.3
Уравнение Д. Бернулли для потока невязкой жидкости без учета потерь энергии, составленное для двух расчетных сечений 1–1 и 2–2 относительно произвольной горизонтальной плоскости сравнения, записывается в следующем виде:
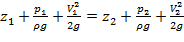 (3.8)
(3.8)
Для понимания геометрического смысла уравнения Бернулли рассмотрим поток в канале с переменным сечением.
z – геометрическая высота или геометрический напор, определяет высоту положения центра тяжести живого сечения потока над произвольной горизонтальной плоскостью сравнения или плоскостью отсчета 0–0;
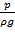 – пьезометрическая высота или пьезометрический напор, представляет высоту такого столба жидкости, который соответствует гидродинамическому давлению в центре тяжести живого сечения потока;
– пьезометрическая высота или пьезометрический напор, представляет высоту такого столба жидкости, который соответствует гидродинамическому давлению в центре тяжести живого сечения потока;
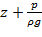 – потенциальный напор;
– потенциальный напор;
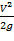 – скоростная высота или скоростной напор;
– скоростная высота или скоростной напор;
V – средняя скорость в живом сечении потока;
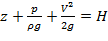 – полный напор.
– полный напор.
Т.к. сечения взяты произвольно, то можно утверждать, что: для идеальной движущейся жидкости сумма трех высот: геометрической, пьезометрической и скоростной есть величина постоянная вдоль потока.
Из уравнения Бернулли:
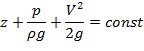
и уравнения расхода:
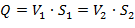
следует, что с уменьшением площади живого сечения потока, скорости течения жидкости увеличиваются, а давления уменьшается, и наоборот.
Энергетический смысл уравнения Бернулли удобно рассматривать в форме удельной энергии, т.е. энергии, отнесенной к единице веса.
z – удельная энергия положения;
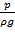 – удельная энергия давления;
– удельная энергия давления;
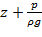 – удельная потенциальная энергия жидкости;
– удельная потенциальная энергия жидкости;
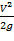 – удельная кинетическая энергия жидкости;
– удельная кинетическая энергия жидкости;
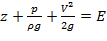 – полная удельная энергия жидкости.
– полная удельная энергия жидкости.
Дата добавления: 2016-06-15; просмотров: 5471;











