Основы теории кристаллизации

ФАЗОВЫЕ ПРЕВРАЩЕНИЯ В СТЁКЛАХ

3.1. Кристаллизация в стёклах

Основы теории кристаллизации

Наблюдения показывают, что новая фаза появляется не сразу во всём объёме исходной фазы. Сначала в отдельных участках материнской стекловидной фазы появляются мелкие зародыши дочерней фазы с упорядоченным расположением частиц. Со временем эти зародыши разрастаются в кристаллическую фазу, распространяющуюся по всему стекла. Теория появления зародышей была в общем виде сформулирована Гиббсом и затем детально разработана Фольмером, Френкелем и другими исследователями.

Во всякой системе, даже находящейся в состоянии термодинамического равновесия, наблюдаются уклонения различных интенсивных свойств от их средних значений.

Например, если Т – средняя температура, то имеются ограниченные локальные участки, где температура Т´ > T или T´´ < T.

ρ – средняя плотность, ρ´ > ρ или ρ´´ < ρ.

С – средняя концентрация, С´ > С или С´´< C.

Эти уклонения интенсивных свойств от их средних значений называются флуктуациями. Они возникают вследствие теплового движения атомов и ионов. Маленькие флуктуации появляются непрерывно, крупные – гораздо реже.

Если возникновение флуктуации не сопровождается появлением поверхности раздела, флуктуацию называют гомофазной. Если флуктуация отделяется от материнской фазы видимой границей раздела, флуктуацию называют гетерофазной.

Вероятность W появления флуктуаций обоих видов выражается уравнением:

,

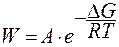А – предэкспоненциальный множитель;

ΔG – изменение энергии Гиббса системы при образовании флуктуации.

Изменение энергии Гиббса можно рассчитать, если известен объём флуктуации:

n = v/V,

n – число молей вещества во флуктуации;

v – объём данной флуктуации;

V – объём одного моля вещества.

Изменение энергии Гиббса при появлении гомофазной флуктуации составляет:

ΔG = n (G₂ – G₁),

G₁ — молярная энергия Гиббса в исходной фазе;

G₂ – молярная энергия Гиббса в новой дочерней фазе.

Если в стеклофазе появляется кристаллоподобная гомофазная флуктуация, то

ΔG = n (G_кр – G_ст),

G_кр – молярная энергия Гиббса кристаллической фазы;

G_ст – молярная энергия Гиббса стеклообразной фазы.

Последние два уравнения характеризуют изменение энергии Гиббса системы при возникновении гомофазной флуктуации. Если возникает гетерофазная флуктуация, то необходимо учитывать энергию межфазной границы:

ΔG = n (G₂ – G₁) + σ∙ω,

σ – свободная энергия единицы поверхности раздела фаз;

ω – площадь поверхности гетерофазной флуктуации.

Для зарождения новой фазы существенны гетерофазные флуктуации. Вероятность W возникновения зародышей определяется, в основном, изменением энергии Гиббса ΔG, т.к. предъэкспоненциальный множитель А мало изменяется при изменении внешних условий.

Допустим, что появляется шаровая гетерофазная флуктуация радиусом r. Её объём и поверхность легко рассчитать:

v = 4/3∙π r³; ω = 4πr².

Молярный объём V выразим через массу моля вещества M и его плотность ρ: V = M/ρ. После подстановок уравнение для изменения энергии Гиббса примет вид:

.

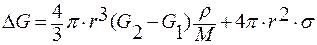Рассмотрим, как изменяется ΔG при различных условиях. Возьмём в качестве меры пересыщения уклонение температуры системы от равновесной.

Т_о – температура равновесного существования двух фаз. Для случая кристаллизации Т_о = Т_пл. Зависимость энергии Гиббса от температуры определяется уравнением:

.

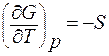Так как энтропия S всегда положительна, то с повышением температуры энергия Гиббса G любого вещества уменьшается (рис.3.1.).

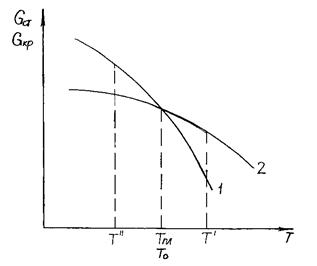
Введём обозначения: 1 – стекло, 2 — кристаллическая фаза.

Рис. 3.1. Изменение энергии Гиббса стекла и кристаллической фазы с температурой

T' > T_пл G_кр–G_ст > 0

Т = Т_пл G_кр = G_ст

T'' > T_пл G_кр–G_ст < 0

Знак первого слагаемого в выражении для ΔG зависит от температуры, а второе слагаемое 4πr²σ всегда положительно.

Т = Т_о – ΔG ~ r² .

Т' > Т_о – с увеличением радиуса r растёт ΔG, причём рост более интенсивный, чем в первом случае, так как добавляется первое слагаемое, пропорциональное r³ (рис.3.2).

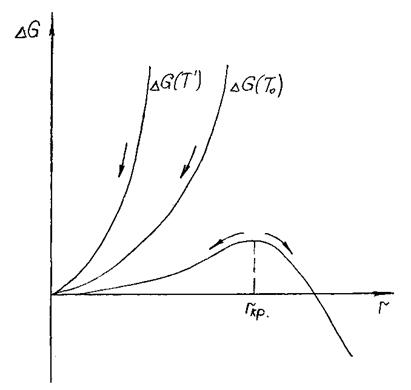
Рис. 3.2. Изменение энергии Гиббса системы с размером

флуктуации, появившейся при различных температурах

Новая фаза живуча, если увеличение её объёма сопровождается уменьшением энергии Гиббса. Если появится флуктуация любого размера r при Т' ≥ Т_о , то её дальнейший рост (r ↑) сопровождается увеличением энергии Гиббса системы. При заданных Р и Т все процессы самопроизвольно могут протекать в сторону уменьшения энергии Гиббса G. Поэтому при Т' ≥ Т_о самопроизвольно идёт распад гетерофазных флуктуаций, они исчезают (r ↓). Все флуктуации, появившиеся при температурах Т' ≥ Т_о растворяются в исходной материнской фазе (r → 0).

При температуре T'' < T_пл первое слагаемое уравнения ΔG = ΔG (r) отрицательно.

G₂ – G₁ < 0; G₂<G₁.

Первое слагаемое уравнения ΔG = ΔG (r) растёт пропорционально r³, второе слагаемое растёт пропорционально r². При малых радиусах превалирует квадратичная парабола, а при больших радиусах основной вклад в изменение ΔG вносит кубическая парабола – первое слагаемое, пропорциональное r³. Так как первое слагаемое имеет знак минус, а второе – плюс, то величина ΔG при увеличении размера флуктуации будет меняться, проходя через максимум.

Если размер флуктуации r < r_кр, то самопроизвольный рост флуктуации невозможен, идет спонтанный распад флуктуации.

Если размер гетерофазной флуктуации r > r_кр, то флуктуация самопроизвольно (спонтанно) растёт, увеличиваясь в размерах. Флуктуации с r > r_кр являются зародышами новой фазы, так как они могут расти самопроизвольно.

Для выявления размера критической флуктуации найдем производную от ΔG по r и приравняет её к нулю.

При r = r_кр производная .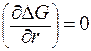

.

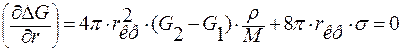
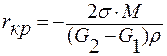Выразим разность энергий Гиббса (G₂ – G₁) через параметры, доступные для измерения.

При Т = Т_о G₂(T_o) = G₁(T_o);

Добавим и вычтем в разности (G₂ – G₁) одну и ту же величину:

G₂(T) – G₁(T) = [(G₂(T) – G₂(T_o)] – [G₁(T) – G₁(T_o)];

Воспользуемся уравнением:

f(x) = f(x_o) + f΄(x_ср)∙(x – x_o); f(x) – f(x_o) = f΄(x_ср)∙(x – x_o),

где f΄(x_ср) – производная в промежуточной точке x_ср между значениями x и x_o: x_ср = (x – x_o)/2.

Так как производная (dG/dT) = - S, то получим

;

.

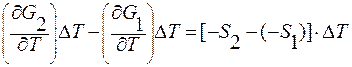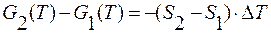S₂ – S₁ = ΔS – изменение энтропии при переходе вещества в новую фазу.

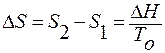- при Т = const

ΔH – тепловой эффект при переходе моля вещества из первой фазы во вторую.

;

.

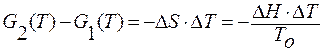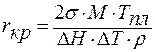Большинство параметров этого уравнения являются физическими постоянными и входят в справочники. Из всех величин наибольшим изменениям могут быть подвергнуты два параметра: межфазное натяжение σ и переохлаждение ΔТ.

М/ρ – молярный объём, вполне определённая величина для данного вещества;

σ – сильно изменяется с введением поверхностно-активных веществ. Межфазное натяжение σ тем меньше, чем ближе состав и структура контактирующих фаз.

Если σ ↓, то r_кр также уменьшается, повышается живучесть новой фазы.

Переохлаждение ΔТ может существенно влиять на r_кр. Однако с уменьшением температуры растёт вязкость среды, что замедляет доставку вещества к растущему зародышу, а это затрудняет его формирование. Поэтому разность температур ΔТ влияет на зародышеобразование только до определённых пределов.

С изменением r_кр существенно меняется работа образования зародыша критического размера.

А_кр = –ΔF_кр, ΔF_кр – изменение свободой энергии Гельмгольца.

Строго говоря, А_кр = –ΔF_кр, но в конденсированных фазах ΔF ≈ ΔG. Поэтому можно найти работу образования критического зародыша, подставив в уравнение для ΔG вместо r критический радиус r_кр:

;

.

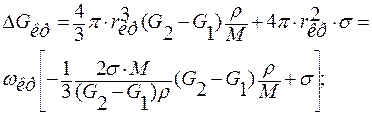
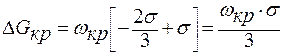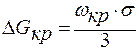Работа образования критического зародыша составляет только 1/3 часть от работы образования его поверхности. Недостающие 2/3∙ΔG_кр покрываются за счет внутренней энергии, за счёт перехода вещества в устойчивое состояние из нестабильной фазы. Так как G_кр<G_ст, то вещество самопроизвольно переходит в фазу с меньшей энергией Гиббса.

.

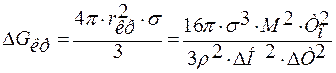ΔG_кр очень сильно зависит от межфазного натяжения σ и от переохлаждения ΔТ, так как имеем σ³ и ΔТ².

.

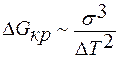σ↓ ΔТ↑ r_кр и ΔG_кр ↓

Выведенные уравнения относятся к сферическим зародышам, однако качественно их можно применять и к появлению зародышей других форм. Влияние σ и ΔТ останется прежним, изменится только коэффициент формы или постоянные величины. Для критического зародыша кубической формы

,

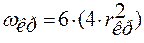где размер ребра куба принят равным 2r, множитель 6 – число граней кубического зародыша. Площадь поверхности куба составит ω_куб=24∙ r², а для шара ω_шар=12,48∙ r².

Наиболее часто выведенные уравнения используются при анализе процессов образования кристаллических зародышей в жидкой фазе. Добавление небольших количеств поверхностно-активных веществ, снижающих σ_ж-тв, позволяет уменьшить критический размер зародыша и работу его образования.