Высокоэластическое состояние

Напомним, что если макромолекула состоит из большого количества отдельных звеньев и существует вращение вокруг связей с сохранением углов и межатомных расстояний, то это гибкая макромолекула.

Существует в этом случае высокая вероятность перехода между гош- и транс- конформациями. Такие молекулы под действием различных воздействий способны менять свою конформацию.

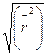
Рис. 17.1. Модель свободно сочлененной цепи (ССЦ)

Среднеквадратичное расстояние между концами цепи 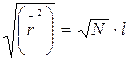гораздо меньше произведения 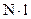, где N – число звеньев, l – длина звена

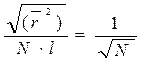
(17.1)

Чем больше число звеньев, тем получается более свернутая цепочка

Среднеквадратичное расстояние является наиболее вероятным расстоянием между концами цепи.

Если начинаем "тянуть" макромолекулу за концы, то молекула растягивается, переходит в менее вероятное состояние. Энтропия при этом уменьшается, тепловое движение будет препятствовать этому. При снятии нагрузки молекула должна возвращаться в свое более вероятное состояние.

Т.е. появляется упругая сила энтропийной природы. В такой макромолекуле заложена способность к большим обратимым деформациям.

Приведем пример, пусть N = 2500, тогда

,

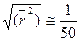тогда получаем, что заложен большой ресурс обратимой деформации – молекула способна удлиняться в 50 раз

Молекула в обычном состоянии находится в форме клубка. Клубок, образованный макромолекулой, способен не только распрямляться, но и сворачиваться. Может образовываться глобула – очень компактно свернутый клубок. Объем клубка может в сотни раз превосходить объем глобулы.

Этими причинами объясняются эластичность полимерных материалов и низкий модуль упругости.

Приведем оценочный расчет упругой силы, возникающей при изменении конформации клубка под действием внешней силы. Вероятность данной конформации с определенным значением 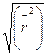(φ(r)) пропорциональна числу путей из N шагов для получения данного 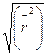. Функция вероятности этого состояния – энтропия (S) пропорциональна lnφ(r). Если принять функцию вероятности по Гауссу 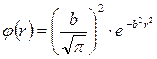, где 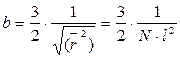, то конформационная энтропия макромолекулы составляет:

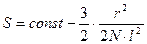(17.2)

Энергия F равна

F= -TS, (17.3)

получаем (в предположении, что при растяжении ∆Н ≈ 0):

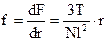(17.4)

Следствия:

1. Эта зависимость подчиняется формально закону Гука:

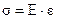, (17.5)

где Е - модуль упругости, ε - деформация

2. Модуль упругости 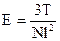, (17.6)

отсюда получаем:

а) При больших N получаем малое Е, система является очень мягкой (макромолекула сопротивляется, но слабо);

б) Чем больше температура, тем это сопротивление больше, модуль упругости увеличивается (у низкомолекулярных веществ жесткость с температурой падает).

Итак, имеем дело с очень рыхлым клубком V_кл ~ 100 ∙ V_гл

Это идеализированная картина, рассматривающая поведение изолированной макромолекулы в вакууме. В реальности мы имеем дело с конденсированным состоянием полимера.

Рассмотрим, какова конформация макромолекул в конденсированной фазе.

Здесь возможны следующие гипотетические представления о возможной конформации макромолекул:

· Сжимаются до глобулярного состояния;

· Сохраняется конформация цепей в виде клубка;

· Образуется промежуточная конформация.

От вида конформации будет зависеть, переносятся ли параметры изолированного клубка при переходе в конденсированное состояние.

Исследования методом рассеяния пучка нейтронов, пропускаемого через образцы сред, содержащих дейтерированные макромолекулы, находящиеся в среде обычных макромолекул того же химического строения, показали, что в среде себе подобных молекулы сохраняют свою исходную невозмущенную конформацию. Это состояние называется θ-конформацией.

Теперь рассмотрим вопрос о том, как свойства вулканизированных каучуков соответствуют параметрам отдельных гибких цепных макромолекул.

Свойства вулканизированных каучуков (резин):

1. Большие деформации (сотни %)

2. Низкие модули упругости:

Е_кауч=10÷100 кг/см²

(у других веществ Е_нмс=10⁴÷10⁸ кг/см²)

3. Объем при растяжении каучуков остается постоянным: происходит перераспределение молекулярных фрагментов в образце, нет изменения межмолекулярных и атомных расстояний (у других веществ объем при растяжении увеличивается)

4. При деформации резин происходит их нагревание (металлы при деформации охлаждаются)

5. Плотности каучуков, коэффициенты теплового и объемного расширения похожи на органические жидкости соответствующей природы.

Таким образом, основные равновесные свойства вулканизированных каучуков достаточно точно совпадают с ожидаемым поведением изолированных гибкоцепных макромолекул, и связаны со способностью изменения их конформаций под действием внешних сил. Однако, возникает важный вопрос о реализации этих возможностей за реальные времена наблюдения.

Деформация полимерного образца развивается во времени по последующему закону:

ε = ε_∞(1 - е ^-t/τ) (17.7)

τ – время релаксации – является параметром, характеризующим скорость реакции образца на механическое воздействие.

Время релаксации показывает, за какое время свойства системы изменились в е (е ≈ 2,718) раз.

t – время воздействия

Если t<<τ, то ε = ε_о; если t > τ, то ε → ε_∞

На рисунке 17.1.2. представлена зависимость деформации от времени воздействия при различных температурах:

ε

Т₁ Т₂ Т₃

Т₄

упругая деформация

t_вр

Т₁ > Т₂ > Т₃ > Т₄

Рис. 17.2. Зависимость деформации от времени воздействия при различных температурах

Зависимость деформации от температуры при различных значениях времени воздействия представляется в следующем виде:

ε

t₁ t₂ t₃

Т_ст1 Т_ст2 Т_ст3 Т

t₁ > t₂ > t₃

Рис. 17.3. Зависимость деформации от температуры при различных значениях времени воздействия

Чем быстрее производится воздействие, тем выше должна быть температура, при которой достигается то же самое значение деформации образца.

ε σ=const

вязко-текучее состояние

сшитый полимер

стекла каучуки, резины

упругая деформация

Т_ст Т₁ Т_тек Т

Рис. 17.4. Зависимость деформации от температуры при условии σ = const

Теперь при условии σ = const и t_набл = constрассмотрим температурную зависимость наблюдаемой деформации образца полимера.

Пусть при температуре Т₁ за время t_набл успевает развиться деформация растяжения клубков (высоко-эластическая деформация) - ε₁. Это значит, что образец ведет себя как мягкое тело. При понижении температуры (Т < Т₁) τ растет и при некоторой температуре (Т_ст) τ > τ_набл деформации клубков развиваться не успевают, и образец ведет себя как твердое стеклообразное тело.

При повышении температуры выше Т₁ (до Т_тек) за время наблюдения, наряду с изменениями конформации клубков (обратимой высокоэластической деформацией), начинается необратимое смещение центров тяжести макромолекул относительно друг друга в направлении действия силы (течение образца). Если макромолекулы в полимерном образце связать в редкую пространственную сетку (вулканизация эластомера), то необратимое течение подавляется, и обратимая высокоэластическая деформация наблюдается до более высоких температур вплоть до температур химического разложения.

Это значит, что при температурах ниже Т_ст – температуры стеклования – полимер находится в твердом стеклообразном состоянии (полимеры в этом состоянии используются как твердые конструкционные материалы – пластики или пластмассы (из них изготавливают листы, пленки, нити, волокна и большое множество других изделий)).

При температурах от Т_ст до Т_тек полимер находится в высокоэластичном состоянии (изготавливают различные изделия из резин (эластомеров))

При температурах от Т_тек – температуры текучести полимера – до температуры химического разрушения полимера если полимер линейный, то может происходить необратимое перемещение макромолекул, как вязкой жидкости, т. е. реализуется его вязко-текучее состояние, используемое для переработки полимеров.

Температуры стеклования и текучести полимера являются важными характеристиками полимеров, т. к. они дают информацию о возможности использования получаемых полимеров и возможности применения различных технологических процессов для их обработки.

Итак, заключаем, что аморфные полимеры могут существовать в 3 физических состояниях – стеклообразном, высокоэластическом и вязко-текучем.

Рассмотрим, как будет меняться зависимость деформации от температуры с увеличением длины молекулы (или молекулярного веса полимера):

ε М₅ М₆ М₇

М₁ М₂ М₃ М₄

Т_ст1Т_ст2Т_ст3 Т_ст4,5,6,7 Т

Рис. 17.5. Зависимость деформации от температуры с увеличением длины молекулы (или молекулярного веса полимера)

С увеличением длины цепи низкомолекулярных аналогов Т_ст растет, а выше Т_ст наблюдается течение образца (кривые 1-3). С достижением некоторой длины цепи зависимость Т_ст от М перестает существовать, и появляется переход в высокоэластическое состояние. Это объясняется тем, что при некотором значении молекулярной массы теряется корреляция положения начала и конца цепи. Изменение конформации в пределах одного сегмента происходит независимо от других сегментов, поэтому далее температура перехода из стеклообразного состояния уже не зависит от молекулярной массы, полимер переходит в высокоэластическое состояние.

Чем быстрее воздействуем на образец, тем более высокая температура необходима для наблюдения высокоэластического состояния; идет перемещение в область высоких температур. Т. о. заключаем, что температура стеклования зависит от скорости воздействия.

Пусть к системе приложена синусоидальная нагрузка:

σ

0 π 2π 3π 4π

ψ

Рис. 17.6. Синусоидальная нагрузка, с которой воздействуют на систему

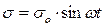(17.8)

Получаем, что для воздействующей системы происходит отставание по фазе на угол ψ, причем релаксационная картина устойчива.

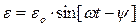(17.9)

Чем больше сдвиг по фазе, тем больше разбаланс; механическая энергия будет переходить в тепло, а не в деформацию.

Происходит отставание во времени, обнаруживается процесс гистерезиса.

Физический смысл явления гистерезиса наглядно демонстрируется на зависимости изменения напряжения от деформации:

σрастяжение полимера

ψ=0

гуковское тело

сокращение полимера

ε

Рис. 17.7. Зависимости изменения напряжения от деформации

Площадь, заключенная между кривыми равна величине энергии механических потерь.

На практике удобнее характеризовать механические потери, прилагая циклическую нагрузку. В этом случае мерой потерь служит Ψ – угол механических потерь, при ψ = 0 (tgψ = 0) – применим закон Гука (напряжение зависит от деформации линейно, 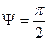для вязких жидкостей и

0 < 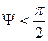для вязко-упругих тел).

В переходной области Т_ст тангенс угла потерь максимален.

Для разных скоростей воздействия будем получать в сопоставимых условиях кривые с максимумами при разных температурах:

tgψ

t₁ t₂ t₃

T

t₁ >t ₂ > t₃

Рис. 17.8. Зависимость tgψ от температуры

Таким образом, скорость воздействия имеет важное значение для определения эластических свойств.

Скорости воздействия на систему сильно влияют на температуру стеклования:

ε

σ=const, t=const

ω₁ ω ω₂

ω₁ < ω < ω₂

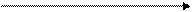
Т_ст1Т_стТ_ст2 Т

Рис. 17.9. Зависимость деформации от температуры при σ=const, t=const

Количественный подход к характеристике вязко-упругих тел полимеров основан на следующих представлениях. При циклической нагрузке на полимер 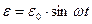, а 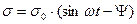где 0 < 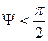. Если математически выразить эту зависимость в виде комплексного числа, то получим: 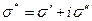, где σ' – действительная, σ'' – мнимая часть.

Модуль вязкоупругого тела:

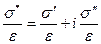или 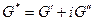(17.10)

Здесь G' – это модуль накопления, показывающий, сколько энергии накапливает полимер при нагрузке и отдает при разгрузке (мера упругости полимера), а G'' – это модуль потерь, являющийся мерой потерянной работы, и, наконец 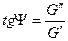. Типичные зависимости G', ɛ и tgψ от температуры и от частоты воздействия представлены на рисунке 17.10.

G', ɛ, tgψ G', ɛ, tgψ

ɛ G'

tgψ tgψ

G' ɛ

Т_ст Т ω

Рис. 17.10. Зависимости G', ɛ и tgψ от температуры и от частоты воздействия

Видно, что зависимости зеркально симметричные, т. е. повышение температуры и снижение частоты воздействия вызывают аналогичные изменения параметров полимера. Это явление называют температурно-временной эквивалентностью (суперпозицией).

Вопросы для самостоятельной проработки:

1. Понятие о гибкости макромолекулы полимера.

2. Связь между структурой полимеров и их свойствами.

3. Назовите основные свойства вулканизированных каучуков.

4. Три физических состояния линейных аморфных полимеров.

5. Факторы, влияющие на величины температуры стеклования и течения полимеров.

6. Релаксационные процессы и их влияние на свойства полимеров.

Задачи для самостоятельного решения

5. Основные физико-механические свойства полимеров

5.1. Термомеханическая кривая

Вопросы 1501 – 1502, 1403 – 1405,1306 – 1308