Частотное распределение
Элементы сырых данных становятся постижимы, когда они сгруппированы в частотное распределение. Чтобы сгруппировать данные, мы должны сначала поделить шкалу, по которой они измерялись, на интервалы, и затем посчитать, сколько элементов приходится на каждый интервал. Интервал, в котором группируются величины, называется групповым интервалом. Решение о том, на сколько групповых интервалов надо разбить данные, не определяется каким-либо правилом, а исходит от решения исследователя.
В табл. П1 показана выборка сырых данных, отражающих показатели 15 учащихся на вступительных экзаменах в колледж. Показатели приведены в том порядке, в каком учащиеся сдавали экзамен (у первого учащегося показатель был 84, у второго — 61 и т. д.). В табл. П2 эти же данные представлены в виде частотного распределения, для которого групповой интервал был установлен равным 10. На интервал от 50 до 59 приходится один показатель, на интервал от 60 до 69 — два и т. д. Заметьте, что большинство показателей приходятся на интервал от 70 до 79 и что ни один показатель не ниже интервала 50-59 или выше интервала 90-99.
Таблица П1. Сырые показатели
84, 61, 72, 75, 77, 75, 75, 87, 79, 51, 91, 67, 79, 83, 69
(Показатели 15 учащихся на вступительных экзаменах в колледж, приведенные в том порядке, в каком учащиеся сдавали экзамен.)
Таблица П2. Частотное распределение
| Групповые интервалы | Число лиц в группе |
| 50-59 | |
| 60-69 | |
| 70-79 | |
| 80-89 | |
| 90-99 |
Показатели из табл. П1, разбитые на групповые интервалы.
Частотное распределение легче понять, когда оно представлено графически. Наиболее широко применяемая графическая форма — это частотная гистограмма; ее пример показан в верхней части рис. П1. Гистограммы составляются путем рисования полос, основания которых задаются групповыми интервалами, а высота — соответствующими частотами групп. Еще один способ представления частотного распределения в графической форме — огибающая частоты, пример которой показан в нижней части рисунка П1. При построении огибающей частоты групп отмечаются напротив середины интервала групп, а затем эти точки соединяются прямыми линиями. Для завершения картины на каждом конце распределения добавляется еще один класс; поскольку у этих классов частота нулевая, оба конца получившейся фигуры окажутся на горизонтальной оси. Огибающая частоты дает ту же информацию, что и частотная гистограмма, но состоит из ряда соединенных отрезков, а не из полосок.
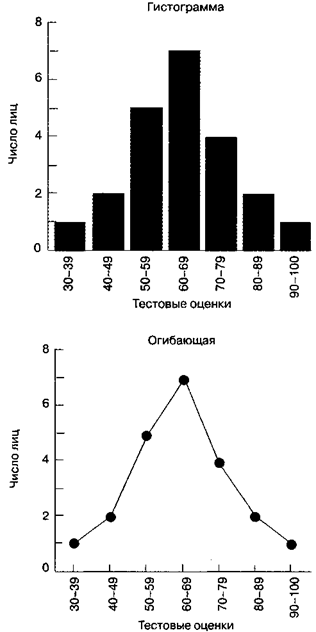
Рис. П1. Частотные графики.Здесь отображены данные из табл. П2. Вверху — частотная гистограмма, внизу — огибающая частоты.
На практике число элементов получается гораздо большим, чем то, что отражено на рис. П1, но на всех рисунках этого приложения показано минимальное количество данных, так чтобы вы могли легко проверить этапы размещения в таблице и на графике.
Меры среднего
Мера среднего — это просто показательная точка на шкале, сжато отражающая особенность имеющихся данных. Обычно используются три меры среднего: среднее значение, медиана и мода.
Среднее значение (или просто среднее) — это знакомое нам арифметическое среднее, получающееся при сложении всех величин и делении полученной суммы на их количество. Сумма сырых величин из табл. П1 равна 1125. Если поделить ее на 15 (общее количество величин), то среднее будет 75.
Медиана — отметка среднего элемента последовательности, полученной путем расположения всех величин по порядку и затем отсчета к середине, начиная с любого конца. Если 15 величин из табл. П1 расположить по порядку от самого большого к самому малому 8-я величина с любого конца будет равна 75. Если исходное количество величин будет четным, то мы просто считаем среднее от тех двух, которые оказываются в середине.
Мода — это самый часто встречающийся показатель в данной выборке. Самая частая величина в табл. П1 — это 75, следовательно, мода этого распределения равна 75.
При нормальном распределении, когда величины распределены поровну с каждой стороны от середины (как на рис. П1), среднее, медиана и мода одинаковы. Это не так для скошенных, или несимметричных, распределений. Предположим, нам надо проанализировать времена отправления утреннего поезда. Обычно поезд отправляется вовремя; случается, он отправляется позже, но он никогда не уходит раньше времени. У поезда с отправлением по расписанию в 08:00 время отправления в течение недели может оказаться таким:
Пн: 08:00
Вт: 08:04
Ср: 08:02
Чт: 08:19
Пт: 08:22
Сб: 08:00
Вс: 08:00
Это распределение времен отправления является скошенным из-за двух запоздавших отправлений; они увеличивают среднее время отправления, но не сильно влияют на медиану и моду.
Важно понять смысл скошенного распределения, поскольку иначе разницу между медианой и средним иногда трудно уловить (рис. П2). Если, например, руководство фирмы и ее профсоюз спорят из-за благосостояния работников, средняя величина расходов на зарплату и их медиана могут сдвинуться в противоположных направлениях. Предположим, фирма поднимает зарплату большинству сотрудников, но урезает зарплату высшим управленцам, которые были слишком высоко на шкале оплаты; тогда медиана зарплаты может подняться вверх, тогда как средняя величина зарплаты снизится. Сторона, стремящаяся показать, что зарплата возросла, выберет в качестве индикатора медиану, а сторона, стремящаяся показать снижение зарплаты, выберет среднее.
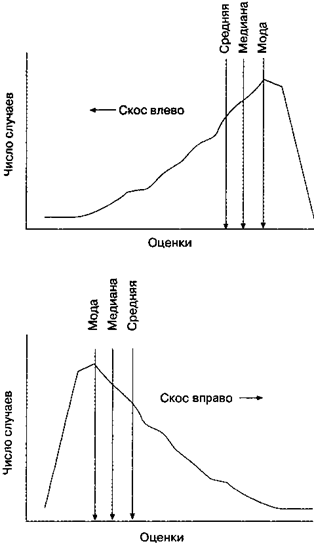
Рис. П2. Кривая скошенного распределения.Заметьте, что скос распределения имеет то направление, в котором спадает его хвост. Заметьте также, что у скошенного распределения среднее, медиана и мода не совпадают; медиана обычно находится между модой и средним.
Меры вариации
Как правило, о распределении нужно знать больше, чем могут показать меры среднего. Нужна, например, мера, которая может сказать, расположен ли пучок величин близко к их среднему или широко разбросан. Мера разброса величин относительно среднего называется мерой вариации.
Показатель вариации полезен как минимум в двух отношениях. Во-первых, он показывает репрезентативность среднего. Если вариация невелика, то известно, что отдельные величины будут близки к среднему. Если вариация большая, то такое среднее нельзя с большой уверенностью использовать в качестве репрезентативной величины. Предположим, что шьется партия готовой одежды без снятия конкретных мерок. Для этого полезно знать средний размер этой группы людей, но также важно знать и разброс их размеров. Зная вариацию, можно сказать, насколько должны варьироваться изготовляемые размеры.
Для иллюстрации посмотрим на данные рис. П3, где приведены частотные распределения показателей вступительных экзаменов для двух классов из 30 учащихся. В обоих классах средний показатель один и тот же — 75, но они очевидно различаются по степени вариации. Показатели всех учащихся из класса А расположены близко к среднему, тогда как показатели учащихся из класса Б разбросаны в широком диапазоне. Нужны какие-то меры, чтобы точнее определить, чем различаются эти распределения. Психологи часто используют три меры вариации: размах, дисперсия и стандартное отклонение.
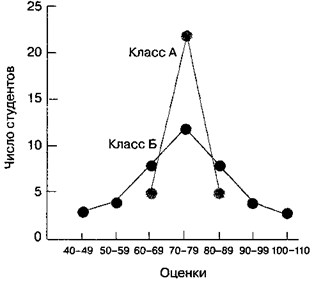
Рис. П3. Пример разной вариации распределений.Как легко видеть, пучок показателей у класса А ближе к среднему, чем показатели класса Б, хотя само среднее в обоих классах идентично — 75. У класса А все показатели попадают между 60 и 89, причем большинство из них приходится на интервал от 70 до 79. У класса Б показатели распределены относительно равномерно по всему диапазону от 40 до 109. Это различие между двумя распределениями в разбросе можно оценить по показателю стандартного отклонения, которое у класса А меньше, чем у класса Б.
Чтобы упростить арифметические вычисления, предположим, что пять учащихся из каждого класса захотели поступить в колледж и что их суммарные оценки на вступительных экзаменах были такие:
Показатели учащихся из класса А:
73, 74, 75, 76, 77 (среднее = 75)
Показатели учащихся из класса Б:
60, 65, 75, 85, 90 (среднее = 75)
Теперь подсчитаем для этих двух выборок меры вариации.
Размах — это разброс между наивысшей и наинизшей величиной. Размах показателей у пяти учащихся из класса А равен 4 (от 73 до 77); размах показателей учащихся класса Б равен 30 (от 60 до 90).
Размах легче подсчитать, но дисперсия и стандартное отклонение используются чаще. Это более чувствительные меры вариации, поскольку они учитывают все величины, а не только крайние величины, как размах. Дисперсия показывает, насколько составляющие распределение величины отстоят от средней величины этого распределения. Чтобы вычислить дисперсию, сначала подсчитаем отклонения каждой величины (d) от среднего, вычтя из среднего каждую величину (табл. П3). Затем надо каждую разницу возвести в квадрат, чтобы не было отрицательных чисел. Наконец, эти отклонения складываются вместе и делятся на общее количество отклонений, давая в результате средний квадрат отклонения. Средний квадрат отклонения называется дисперсией. Проделав это с данными из рис. П3, мы обнаружим, что дисперсия у класса А равна 2,0, а у класса Б — 130. Очевидно, что у класса Б вариативность показателей значительно сильнее.
Таблица П3. Вычисление дисперсии и стандартного отклонения
Оценки Класса А (Среднее = 75)
| d | d2 | |
| 77-75 | ||
| 76-75 | ||
| 75-75 | ||
| 74-75 | -1 | |
| 73-75 | -2 |
Сумма d2 = 10
Дисперсия = среднее по d2 = 10 / 5 = 2,0
Стандартное отклонение (σ) = 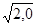 = 1,4
= 1,4
Оценки Класса Б (Среднее = 75)
| d | d2 | |
| 90-75 | ||
| 85-75 | ||
| 75-75 | ||
| 65-75 | -10 | |
| 60-75 | -15 |
Сумма d2 = 650
Дисперсия = среднее по d2 = 650 / 5 = 130
Стандартное отклонение (σ) = 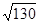 = 11,4
= 11,4
Неудобство дисперсии состоит в том, что она выражена в единицах измерения, возведенных в квадрат. Поэтому величина дисперсии, равная 2 у класса А, не означает, что его усредненные показатели отличаются от среднего на 2 пункта. Она показывает, что 2 — это результат усреднения возведенных в квадрат значений, на которые показатели отличаются от среднего. Чтобы получить меру отклонения, выраженную в первоначальных единицах измерения (в данном случае это количество единиц, набранных на экзамене), надо просто извлечь из дисперсии квадратный корень. Результат называют стандартным отклонением. Оно обозначается греческой буквой σ (сигма), используемой также в некоторых других статистических вычислениях, которые мы обсудим вкратце. Стандартное отклонение вычисляется по следующей формуле:
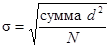
Пример вычисления стандартного отклонения.(табл. П3). Показатели выборок из двух классов представлены в виде, удобном для вычисления стандартного отклонения. На первом этапе вычитаем среднее из каждого показателя (среднее = 75 в обоих классах). В результате получаем положительные величины d для показателей, которые больше среднего, и отрицательные для тех, которые меньше его. Когда полученные величины будут возведены в квадрат, знак минус пропадет (следующая колонка в табл. П3). Возведенные в квадрат разности складываются и делятся на N — количество элементов выборки, в нашем случае N = 5. Извлекая квадратный корень, получаем стандартное отклонение. [В этом ознакомительном изложении мы везде будем использовать σ (сигма). Однако в научной литературе для обозначения стандартного отклонения выборки используется маленькая буква s, а через а обозначают стандартное отклонение для всей группы. Кроме того, при вычислении стандартного отклонения для выборки (s) сумма всех d2 делится не на N, а на N-1. В случае достаточно больших выборок, однако, использование N-1 вместо N мало влияет на величину стандартного отклонения. Для упрощения объяснений мы не будем различать здесь стандартное отклонение выборки и группы и используем для них одну и ту же формулу. Обсуждение этого момента см. в: Phillips (1992).]
Дата добавления: 2019-12-09; просмотров: 883;











