Относительный покой жидкости

Как отмечалось выше, жидкость может находиться в абсолютном или относительном покое. Относительный покой можно наблюдать при движении жидкости вместе с сосудом. В этом случае на нее, кроме силы тяжести, действуют и другие силы, а сама жидкость находится в покое относительно стенок сосуда.

Одним из примеров является цилиндрический сосуд с жидкостью, который вращается вокруг своей вертикальной оси (рис. 20).

Рассмотрим силы, действующие на частицу жидкости.

Центробежная сила в точке М:

,

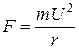где 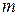– масса жидкости;

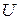– окружная скорость;

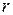– радиус вращения.

Окружная скорость равна:

,

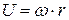где 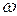– угловая скорость вращения.

Рисунок 20 – Относительный покой

Тогда сила .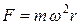

Но при единичной массе единичная сила равна центростремительному ускорению .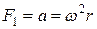

Из уравнения Эйлера 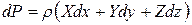найдем проекции центростремительного ускорения на координатные оси:

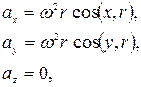
где

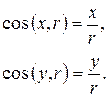
Откуда .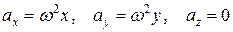

Проекции ускорения силы тяжести: 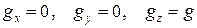, а сумма проекций ускорений массовых сил: .

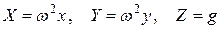Уравнение Эйлера преобразуется к следующему виду:

.

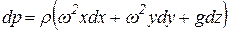Проинтегрировав это уравнение, получим:

,

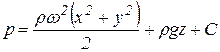но 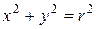и тогда уравнение примет вид:

.

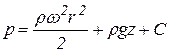Определим постоянную интегрирования 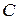. В точке О на свободной поверхности 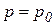, поэтому 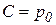, тогда:

.

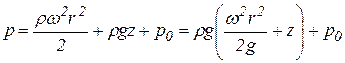С помощью этой формулы можно определить гидростатическое давление в любой точке жидкости, находящейся в сосуде.

Уравнение свободной поверхности получим при :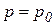

.

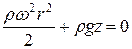Свободная поверхность представляет собой параболоид вращения. Из уравнения свободной поверхности получим:

.

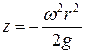По этой зависимости мы можем определить возвышение 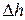для любой точки свободной поверхности, так как ось направлена вниз .

.

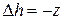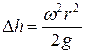Уравнение устанавливает связь между возвышением 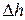и угловой скоростью вращения 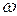, что и используется при расчете и конструировании (например, центрифуг, сепараторов и т. п.).