Общие понятия оптимизационной задачи
На предприятиях ресторанного хозяйства решается множество задач, которые можно оптимизировать. Например, задача планирования общей деятельности, составление производственной программы предприятия, рационализация транспортных расходов, распределение работы на предприятии и его структурных подразделениях между работниками, оптимизация расходов и т.п. Суть методов оптимизации заключается в том, чтобы, исходя из наличия определенных ресурсов, выбрать такой способ их использования (распределения), при котором будет обеспечен минимум или максимум показателя, который интересует. Необходимым условием использования оптимального подхода к планированию (принципа оптимума) является гибкость, альтернативность ситуации, в условиях которой необходимо принимать управленческие решения.
Оптимальное программирование можно применять лишь к таким задачам, при решении которых оптимальный результат достигается лишь в виде точно сформулированной цели и при определенных ограничениях В постановку задачи обычно входит некоторая математически сформулированная система взаимозависимых факторов, ресурсы и условия, ограничивающие характер их использования.
Задача становится разрешимой при введении в нее определенной оценки как для взаимозависимых факторов, так и для ожидаемых результатов. Следовательно, оптимум результата задачи программирования имеет относительный характер. Этот результат оптимален только с точки зрения тех критериев, которыми он оценивается, и ограничений, введенных в задаче. Из этого следует, что для любых задач оптимального программирования характерны три следующих момента:
1) наличие системы взаимосвязанных факторов;
2) строго определенный критерий оценки оптимума;
3) точная формулировка условий, ограничивающих использование ресурсов или факторов.
Из многих возможных вариантов выбирается альтернативная комбинация, отвечающая всем условиям, введенным в задачу, и обеспечивающая минимальное или максимальное значение выбранного критерия оптимума. Решение задачи достигается применением определенной математической процедуры, которая заключается в последовательном приближении рациональных вариантов, соответствующих выбранной комбинации факторов, до единого оптимального плана.
Для численного решения уравнений с несколькими неизвестными и ограничениями в Excel существует инструмент Поиск решения.
Если целевая функция и ограничения линейные, то решение заключается в нахождении множества чисел (х1, х2 .. хn), которые минимизируют (максимизируют) линейную целевую функцию f(х1, х2 .. хn)= c1х1+c2х2+. +cnхn при m<n линейных ограничениях-уравнениях аi1х1+аi2х2+. +аinхn (где i=1,2...m) и n линейных неравенствах хk>=0 (где k=1, 2 ... n).
Алгоритм решения оптимизационной задачи с несколькими неизвестными такой:
- экономическая постановка (анализ задачи, определение свойств, параметров, ограничений);
- математическая постановка (математическое описание модели, введение обозначений, ограничений, и построение целевой функции);
- реализация задачи в среде Microsoft Excel.
6.2 Основные типы задач планирования
Задача оптимизации использования ресурсов(задача планирования производства).
В математической поставке задача формулируется таким образом. Обозначим Xj (j=1,2.,n) – число единиц продукции Pj, запланированных к производству; bi (i=1,2.,m) – запас ресурса Si; aij – число единиц ресурса Si, затраченного на изготовление единиц продукции Pj (числа aij – коэффициенты прямых затрат, которые называют технологическими коэффициентами); cj – доход от реализации единицы продукции Pj. Тогда математическая модель задачи об использовании ресурсов в общей постановке примет вид: найти такой план X=(x1, x2,.xn) выпуска продукции, который удовлетворит системе
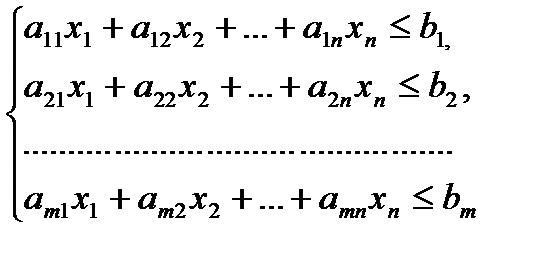
и условии
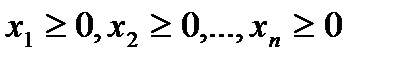 ,
,
при котором функция
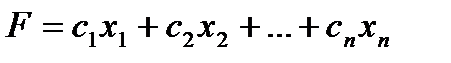
принимает максимальное значение.
Рассмотрим конкретную задачу.
Для изготовления двух видов продукции P1 и P2 используют четыре вида ресурсов S1, S2, S3, S4. Запасы ресурсов, число единиц ресурсов, потраченных на изготовление единицы продукции, приведены в табл. 6.1 (цифры условные).
Цена реализации единицы продукции Р1 и Р2 соответственно, и составляет 2 и 3 у.д.е..
Необходимо составить такой план производства продукции, при котором доход от реализации будет максимальным.
Таблица 6.1 – Данные для решения задачи
| Вид ресурса | Запас ресурса | Число единиц ресурсов, затраченых на изготовление единицы продукции | |
| P1 | P2 | ||
| S1 | |||
| S2 | |||
| S3 | - | ||
| S4 | - |
Составим оптимизационную модель задачи.
Обозначим х1, х2 – число единиц продукции соответственно Р1 и Р2, запланированных к производству. Для их изготовления (табл. 1) нужно (1* х1+3* х2) единиц ресурса S1, (2* х1+1* х2) единиц ресурса S2, (1* х2) единиц ресурса S3 (3* х1) единиц ресурса S4. Поскольку ресурсов потребления S1, S2, S3, S4 не должно превышать их запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выражается системой неравенств:
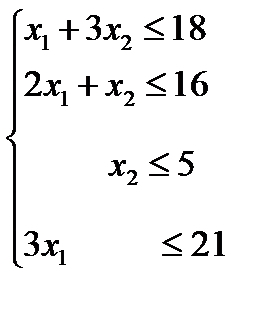
Переменные положительные x1³0, x2³0.
Суммарная доход F от реализации продукции составляет:
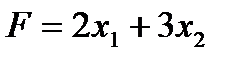 .
.
Задача оптимизации составления рациона(задача о диете, задача о смесях).
Обозначим xj (j=1,2., n) – число единиц корма n - го вида; bi (i=1,2., m) – необходимый минимум содержания в рационе питательного вещества Si; aij – число единиц питательного вещества Sij в единице корма j-го вид; cj - стоимость единицы корма j-го вида. Математическая модель задачи составления рациона в общей постановке примет вид. Найти такой рацион X=(x1, x2.,xj,.,xn), удовлетворяющий системе:
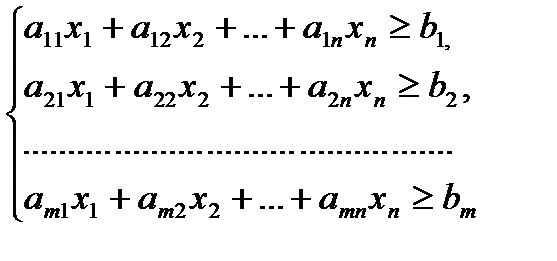
и условию
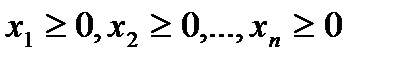 ,
,
при котором функция
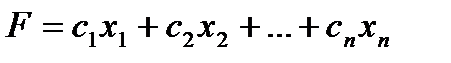
принимает минимальное значение.
Рассмотрим конкретную задачу.
Имеется два вида корма I и II, содержащие питательные вещества (витамины) S1, S2, S3, содержащих. Содержание числа единиц питательных веществ в 1 кг каждого вида корма, необходимый минимум питательных веществ приведен в табл. 6.2 (цифры условные).
Таблица 6.2 – Данные для решения задачи
| Питательные вещества (витамины) | Необходимый минимум питательных веществ | Число единиц питательных веществ в 1 кг корма | |
| I | II | ||
| S1 | |||
| S2 | |||
| S3 |
Стоимость 1 кг корма I и II соответственно равна 4 и 6 у.д.е.
Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание каждого вида питательных веществ было бы не менее установленного предела.
Составим оптимизационную модель задачи.
Обозначим x1, x2 – количество кормов I и II, входящих в дневной рацион. Тогда этот рацион будет включать (3* x1+1* x2) единиц питательного вещества S1, (1* x1+2* x2) единиц веществ S2, (1* x1+6* x2) единиц питательного вещества S3. Так как содержание питательных веществ S1, S2, S3 в рационе должно быть не менее соответственно 9, 8 и 12 единиц, то получим систему неравенств:
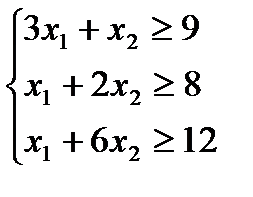 (1)
(1)
Переменные положительные x1³0, x2³0.
Общая стоимость рациона F составит:
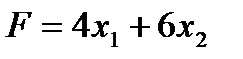 . (2)
. (2)
Задача оптимизации транспортных затрат (задача коммивояжёра)
Для математической постановки транспортной задачи в общей постановке обозначим через сіј коэффициенты затрат, через Mi – мощности поставщиков, через Nj – мощности потребителей, (i=1,2.,m)., (j=1,2.,n, m – число поставщиков, n – число потребителей. Тогда система ограничений принимает вид:
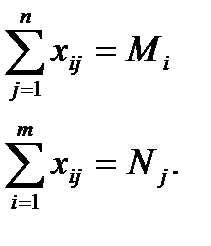 (7)
(7)
Система (7) включает в себя уравнения баланса по строкам и по столбцам.
При этом суммарная мощность поставщиков равна суммарной мощности потребителей, то есть
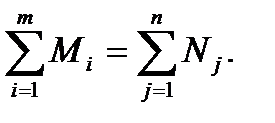
Целевая функция в данном случае следующая:
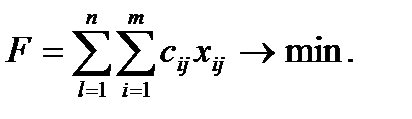 (8)
(8)
Таким образом, на множестве положительных решений системы ограничений (7) найти такое решение, при котором значение целевой функции (8) будет минимальное.
Рассмотрим конкретную задачу.
Есть три поставщика и четыре потребителя. Мощность поставщиков и спрос потребителей, а также затраты на перевозку единицы груза для каждой пары «поставщик - потребитель» сведены в таблицу поставок (табл. 6.3).
Таблица 6.3 – Данные для решения задачи
| Поставщик | Мощность поставщиков | Потребители и их спрос | ||||
В левом верхнем углу произвольной (i,j) ячейки стоит коэффициент затрат – затраты на перевозку единицы груза от i-го поставщика до j-го потребителя. Задача формулируется таким образом: найти объемы перевозок для каждой пары «поставщик - потребитель» так, чтобы: мощности всех поставщиков были реализованы, спросы всех потребителей были удовлетворены, суммарные затраты на перевозку были бы минимальны. Обозначим через xij объем перевозки от i-го поставщика до j-го потребителя. Заданные мощности поставщиков и спросы потребителей накладывают ограничения на значения неизвестных xij. Чтобы мощность каждого из поставщиков была реализована, необходимо составить уравнения баланса для каждой строки таблицы поставок:
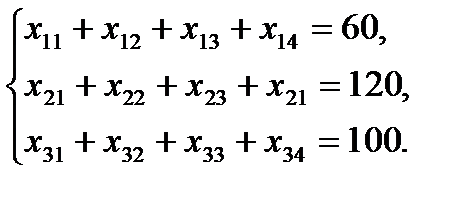
Аналогично, чтобы спрос каждого из потребителей был удовлетворен, подобные уравнения баланса составляются для каждого столбца таблицы поставок:
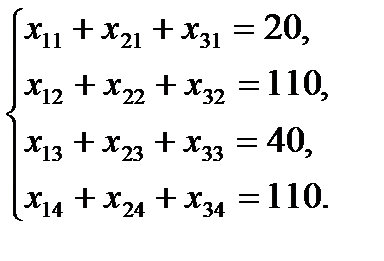
Очевидно, что объем перевозимого груза не может быть отрицательным, поэтому следует ввести ограничение положительности переменных: xij ≥0.
Суммарные затраты F на перевозку выражаются через коэффициенты затрат следующим образом:
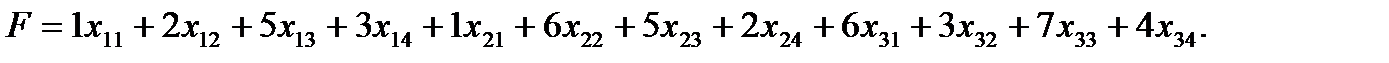
Дата добавления: 2019-12-09; просмотров: 748;











