Методические указания по выполнению задачи 1

Математическая постановка. Обозначим x_j – количество блюд j-го типа (j=1,2,3,4), которые планируется выпускать. При этом будут использованы 1,3x₁+1,3x₂+1,7x₃+0,9х₄ единиц первого сырья; 2,1x₁+1,1x₂+3x₃+1,7х₄ единиц второго сырья; 0,9х₁+2х₂+1,4х₃+2,1х₄ единиц третьей сырья. Исходя из запасов сырья различного вида получим систему ограничений.

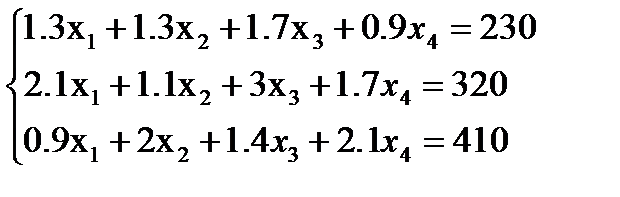(1)

Количество блюд не может быть отрицательным, поэтому

x₁≥0; x₂≥0; x₃≥0; x₄≥0. (2)

Стоимость реализации блюда 1 составит 21,1x₂ руб., стоимость реализации блюда 2 – 21,1x2 грн., стоимость реализации блюда 3 – 9,56x₃ руб., стоимость реализации блюда 4 – 11,34х4 руб. Тогда целевая функция будет иметь вид:

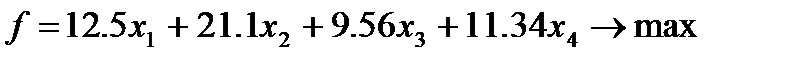(3)

Итак, математическая модель задачи оптимального планирования выпуска блюд: найти такой план выпуска блюд, удовлетворяющий системе (1) и условию неотрицательности (2), при котором функция (3) принимает максимальное значение.

Реализация задачи в среде Microsoft Excel. Построим на листе Microsoft Excel начальную таблицу, как показано на рис. 6.1.

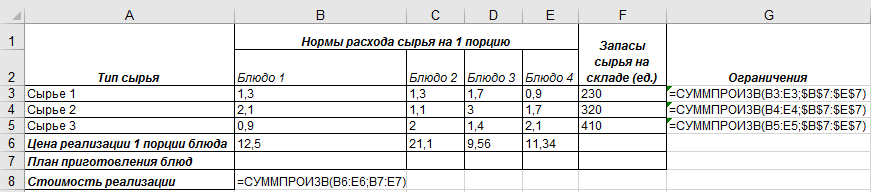
Рис. 6.1 – Образец заполнения исходной таблицы

В ячейках G3:G6 сформируем заданные ограничения с помощью математической функции СУММПРОИЗВ, аргументами которой выступают массивы соответствующих данных о количестве использованного сырья каждого вида.

В ячейке В8 построим целевую функцию с помощью СУММПРОИЗВ, аргументами которой выступают массивы соответствующих данных о стоимости реализации.

Для решения поставленной задачи воспользуемся надстройкой «Поиск решения». Для этого следует перейти на вкладку Данные и заполнить диалоговое окно, как показано на рис. 6.2.

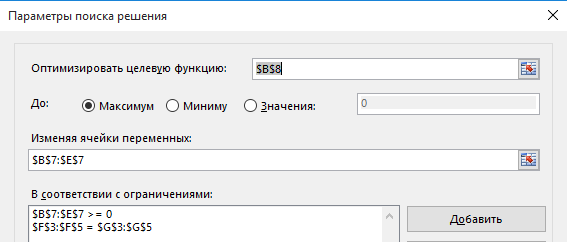
Рис. 6.2 – Образец заполнения диалогового окна «Поиск решения»

В результате выполнения определенного количества итераций получаем следующие результаты (рис. 6.3): для получения максимальной стоимости реализации блюд – 3188 руб. и использования сырья в рамках ограничений необходимо выпускать 21 порцию блюда 1, 79 порций блюда 2 и 111 порций блюда 4.

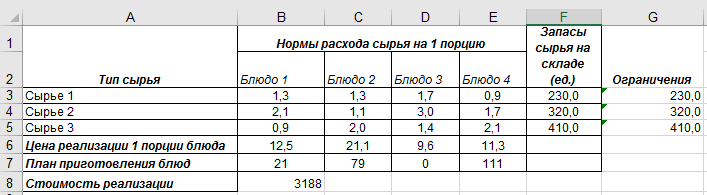
Рис. 6.3 – Результат поиска решения

Задание 2 (Транспортная задача)

Есть четыре ресторана, каждый из которых имеет определенный спрос на продукцию, и три поставщика, которые могут обеспечить определенным количеством продукции. В табл. 6.5 приведены затраты на перевозку единицы продукции каждым поставщиком каждому ресторану.

Таблица6.5 – Данные для решения задачи 2

Составить план поставок таким образом, чтобы общие затраты на перевозки были минимальными.

Математическая постановка. Обозначим х_іј – количество продукции, которую необходимо доставить i-м поставщиком j-ому ресторану. План перевозки задается матрицей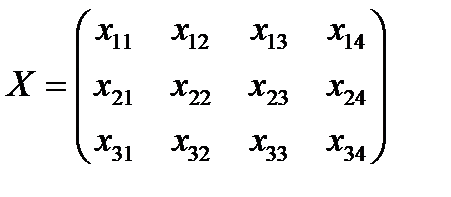

Суммарное количество продукции, которую могут доставить поставщики, равно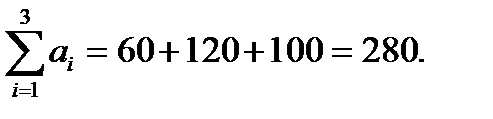

Суммарное количество продукции, которая необходима ресторана, равно

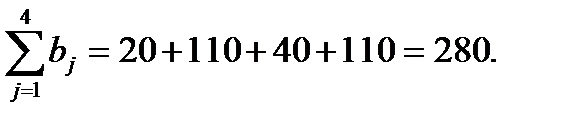
Как видим, обе суммы совпадают, значит, задача закрыта, то есть, спрос ресторанов равняется возможностям поставщиков:

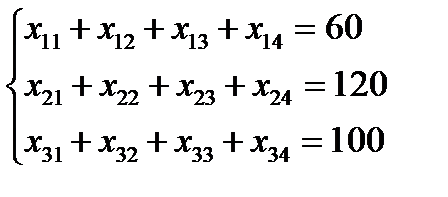(4)

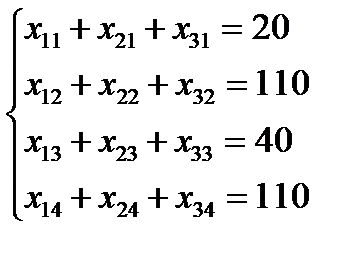(5)

Количество продукции не может быть отрицательной, поэтому

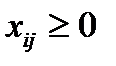(i=1,2,3; j=1,2,3,4) (6)

Суммарные затраты на перевозку продукции рассчитываются следующим образом:

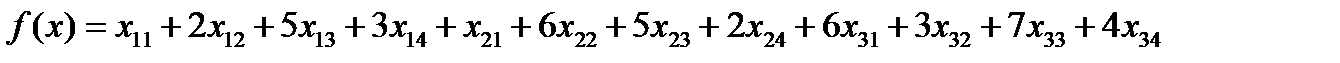(7)

Итак, математическая модель задачи оптимального планирования превезення: найти такой план перевозки, удовлетворяет системе (4), (5) и условию (6), при котором целевая функция (7) принимает минимальное значение:

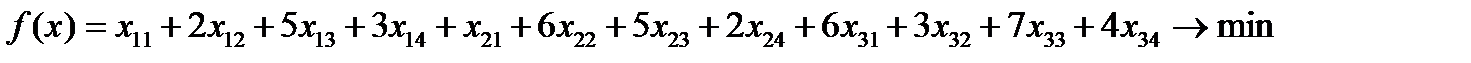
Реализация задачи в среде Microsoft Excel. Построим на листе Microsoft Excel начальную таблицу, как показано на рис. 6.4.

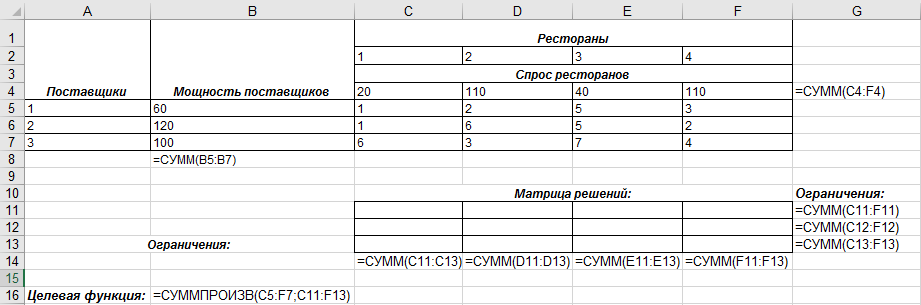
Рис. 6.4 – Образец заполнения исходной таблицы

В ячейках G11:G13 и С14:F14 сформируем заданные ограничения с помощью математической функции СУММ, аргументами которой выступают массивы соответствующих данных о количестве продукции, которую необходимо перевезти.

В ячейке В16 построим целевую функцию с помощью СУММПРОИЗВ, аргументами которой выступают массивы соответствующих данных о стоимости перевозки, соответствующих плану перевозки.

Для решения поставленной задачи воспользуемся надстройкой «Поиск решения», заполним диалоговое окно, как показано на рис. 6.5.

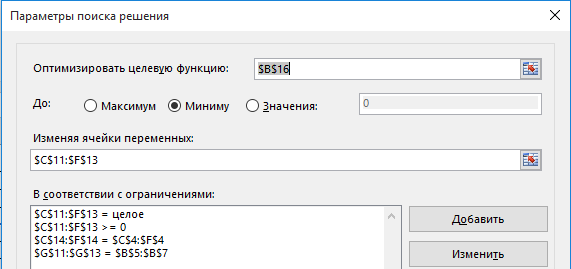
Рис. 6.5 – Образец заполнения диалогового окна «Поиск решения»

В результате выполнения определенного количества итераций получим следующие результаты (рис. 6.6): для получения минимальных затрат на перевозки – 760 ден. ед. и обеспечить необходимым количеством продукции рестораны, необходимо выполнить план перевозки, полученный в диапазоне С11:F13.

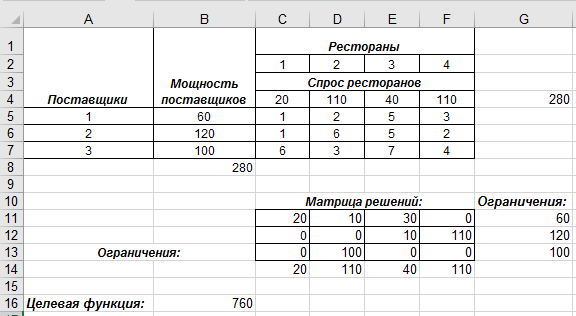
Рис. 6.6 – Результат поиска решения