Системы с подчиненным регулированием координат
В настоящее время наибольшее распространение получили системы управления с подчиненным регулированием координат.

Рис 2.12. Структурная схема привода с подчиненным регулированием координат
Система состоит из нескольких вложенных один в другой контуров. Число контуров равно числу регулируемых координат. Регуляторы включены последовательно. Каждый внешний регулятор является задающим по отношению к внутреннему, кроме того, на вход регулятора подается сигнал ОС по регулируемой координате. В этой системе удобно осуществлять настройку регулятора, поскольку каждый контур, начиная с внутреннего, можно рассматривать независимо. [2, 4, 5, 11]
2.3.1. Особенности выбора регуляторов в системе с подчиненным регулированием координат
Методика расчета систем с подчиненным регулированием основана на том, что контур регулирования должен содержать только одну большую постоянную времени. В этом случае регулятор подбирают таким образом, чтобы при последовательном включении его с соответствующим звеном системы была скомпенсирована большая постоянная времени объекта регулирования и взамен в контуре действовала бы существенно меньшая постоянная времени. Результирующее эквивалентное звено, состоящее из последовательно включенных регулятора и объекта, должно быть интегрирующим, то есть:
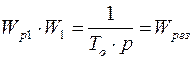 . (2.20)
. (2.20)
Рассмотрим конкретные примеры:
1-й пример. Объект представляет собой интегрирующее звено.
а) 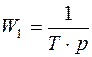 , если регулятор пропорциональный, то
, если регулятор пропорциональный, то 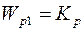 , тогда имеем
, тогда имеем 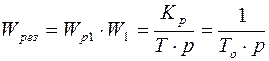 ,
,
где 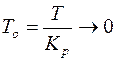 при
при 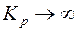 .
.
Передаточная функция замкнутого контура имеет вид:
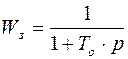 .
.
б) 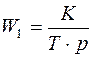 =>
=> 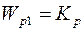 и =>
и => 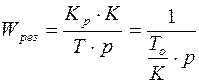 ,
,
где 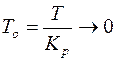 при
при 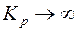 .
.
В этом случае 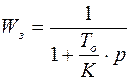 .
.
2-й пример. Объект представляет собой апериодическое звено.
а) 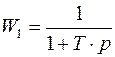 =>
=> 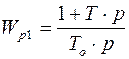 и=>
и=> 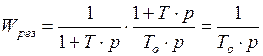 .
.
В результате 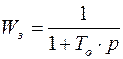 .
.
б) 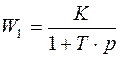 =>
=> 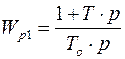 и=>
и=> 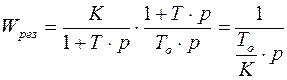 .
.
В этом случае 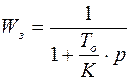 .
.
В системах подчиненного регулирования используются четыре вида регуляторов:
1) П-регуляторы: 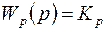 ,
,
2) И-регуляторы: 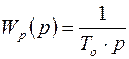 ,
,
3) ПИ-регуляторы: 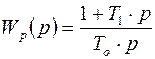 ,
,
4) ПИД-регуляторы: 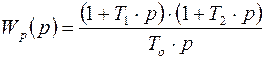 .
.
Когда необходимо компенсировать две большие постоянные времени используется ПИД-регулятор.
Такая методика позволяет обеспечивать единый подход к синтезу регуляторов в каждом из контуров. Некоторые сложности при использовании данной методики вносит ДПТ НВ, за счет наличия внутренней ОС по ЭДС.
 а)
а)
б)
Рис.2.13. Структурная схема двигателя с ОС по ЭДС до (а) и после переноса ОС (б)
Перенос точки ОС не влияет на передаточную функцию Д, но и не дает нужного эффекта, так как в этом случае объект имеет две большие постоянные времени.
Поэтому для упрощения пренебрегают ООС по ЭДС. Тогда передаточная функция Д будет иметь вид:
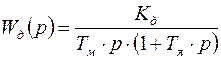 . (2.21)
. (2.21)
Конечно, это приводит к определенной погрешности, но она не существенно влияет на результаты расчета.
Дата добавления: 2016-06-15; просмотров: 4948;











