Выборочные характеристики вариационных рядов

Определение. Совокупность n независимых одинаково распределенных случайных величин 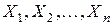называется выборкой, соответствующей распределению случайной величины .

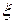Определение. Пусть 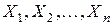‑ выборка из распределения с теоретической функцией распределения 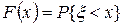, 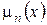‑ число элементов выборки, строго меньших x. Эмпирической функцией распределения (ЭФР) называется функция

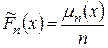. (7.1)

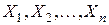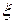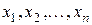Пусть ‑ выборка из распределения случайной величины , а – реализация этой выборки, т.е. наблюдавшиеся значения.

Определение. Выборочным средним называется величина

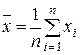. (7.2)

Если данные представлены в виде точечного или интервального вариационного ряда, то для вычисления 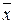используют формулу:

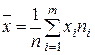, (7.3)

где – количество групп в точечном или интервалов в интервальном вариационных рядах, 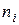– частота, т.е. количество элементов выборки, принадлежащих 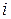-той группе или 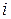-тому интервалу, 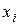– варианта для точечного ряда и середина 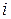-того интервала для интервального ряда.

Определение.Выборочной дисперсией (смещенной) называется величина

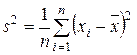. (7.4)

Она характеризует квадрат отклонения в среднем каждой величины выборки от выборочного среднего. Величина 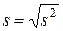называется среднеквадратическим отклонением величин выборки от выборочного среднего.

Определение.Выборочной дисперсией (несмещенной) называется величина

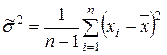. (7.5)

Очевидно, что смещенная и несмещенная выборочные дисперсии связаны формулой

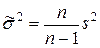. (7.6)

Если данные представлены в виде точечного или интервального вариационного ряда, то для вычисления 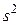используют формулу:

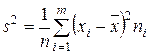, (7.7)

или

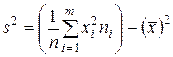, (7.8)

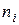где – количество групп в точечном или интервалов в интервальном вариационных рядах, – частота, т.е. количество элементов выборки, принадлежащих 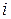-той группе или 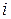-тому интервалу, 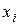– варианта для точечного ряда и середина 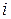-того интервала для интервального ряда.