Точность импульсных систем
Точность замкнутой импульсной системы (рис. 1.3) в дискретные моменты времени 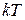 определяется сигналом ошибки (рассогласования)
определяется сигналом ошибки (рассогласования) 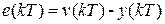 , который характеризует текущую ошибку. Для оценки точности более удобно ввести, как это сделано для непрерывных систем, понятие установившейся ошибки
, который характеризует текущую ошибку. Для оценки точности более удобно ввести, как это сделано для непрерывных систем, понятие установившейся ошибки 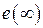 , которая определяется для достаточно больших моментов времени
, которая определяется для достаточно больших моментов времени 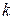 после затухания переходной (свободной) составляющей процессов и в отличие от текущей ошибки часто является числом. Итак, при вычислении
после затухания переходной (свободной) составляющей процессов и в отличие от текущей ошибки часто является числом. Итак, при вычислении 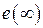 будем полагать, что
будем полагать, что 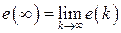 .
.
Изображение сигнала ошибки и изображение входа связаны соотношением
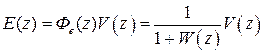 ,
,
где передаточную функцию разомкнутой системы будем брать в форме (1.22)
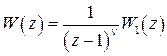 .
.
Обычно оценивается точность импульсной системы на два вида воздействий: полиномиального 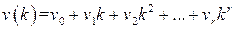 и гармонического
и гармонического 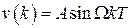 .
.
Частными случаями полиномиального воздействия являются единичная ступенчатая функция (скачок по положению) 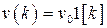 , линейное воздействие (скачок по скорости)
, линейное воздействие (скачок по скорости) 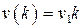 и квадратичное воздействие (скачок по ускорению)
и квадратичное воздействие (скачок по ускорению) 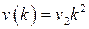 .
.
В теории 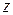 -преобразования существует теорема о конечном значении решетчатой функции (оригинала)
-преобразования существует теорема о конечном значении решетчатой функции (оригинала) 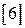
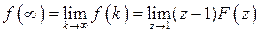 .
.
Используя эту теорему, можно написать
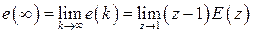 , (1.57)
, (1.57)
где 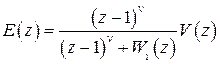 .
.
Рассмотрим частные случаи. Пусть 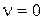 ,
, 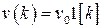 , тогда
, тогда 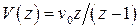 и из (1.57) нетрудно получить
и из (1.57) нетрудно получить 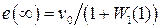 . Т.к.
. Т.к. 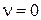 соответствует статической системе, то такую ошибку называют статической.
соответствует статической системе, то такую ошибку называют статической.
Пусть 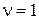 ,
, 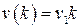 , тогда
, тогда 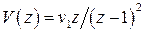 и из (1.57) получим
и из (1.57) получим 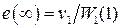 . Такую ошибку будем называть скоростной. Нетрудно проверить, что в данном случае статическая ошибка будет равно нулю.
. Такую ошибку будем называть скоростной. Нетрудно проверить, что в данном случае статическая ошибка будет равно нулю.
Пусть 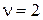 , статическая и скоростная ошибки будут равны нулю, появится ошибка по ускорению. При этом все ошибки будут обратно пропорциональны величине
, статическая и скоростная ошибки будут равны нулю, появится ошибка по ускорению. При этом все ошибки будут обратно пропорциональны величине 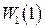 .
.
Итак, можно сделать вывод, который является общим для импульсных систем: точность системы тем выше (ошибки тем меньше), чем выше порядок астатизма системы и больше величина 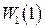 . Так как
. Так как 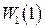 прямо пропорциональна коэффициенту усиления
прямо пропорциональна коэффициенту усиления 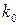 линейной, непрерывной части системы
линейной, непрерывной части системы 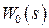 , то увеличение
, то увеличение 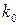 будет приводить к повышению точности импульсной системы.
будет приводить к повышению точности импульсной системы.
Точность системы в установившихся режимах также можно описывать по коэффициентам ошибок 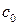 ,
, 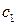 , …, которые имеют аналогичный непрерывным системам смысл и определяются по выражению
, …, которые имеют аналогичный непрерывным системам смысл и определяются по выражению 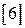 :
:
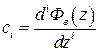 ½
½ 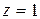 ,
, 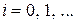 . (1.58)
. (1.58)
В частности для системы с астатизмом 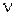 -го порядка
-го порядка 
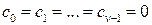 .
.
Рассмотрим анализ точность системы при воспроизведении гармонического сигнала 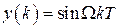 , амплитуду которого будем полагать равной единице. Тогда в соответствии с (1.43) в установившемся режиме на выходе замкнутой системы сигнал будет иметь вид
, амплитуду которого будем полагать равной единице. Тогда в соответствии с (1.43) в установившемся режиме на выходе замкнутой системы сигнал будет иметь вид
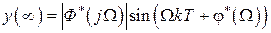 , (1.59)
, (1.59)
а ошибка в установившемся режиме будет
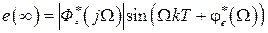 , (1.60)
, (1.60)
где 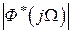 ,
, 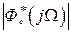 ,
, 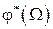 ,
, 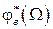 - соответствующие значения модулей и сдвигов фаз, определенные по частотным характеристикам
- соответствующие значения модулей и сдвигов фаз, определенные по частотным характеристикам 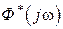 ,
, 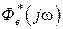 .
.
Обычно в теории систем автоматического управления считают, что ошибки воспроизведения гармонического сигнала по фазе не имеют существенного влияния на работу САУ. Ошибки воспроизведения амплитуды из (1.59), (1.60) будут
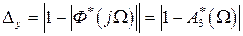 ,
,
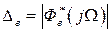 . (1.61)
. (1.61)
Обычно 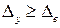 , однако в диапазоне низких частот при малом
, однако в диапазоне низких частот при малом 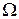 можно считать
можно считать 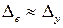 .
.
Так же как и для непрерывных систем, для замкнутой импульсной системы можно ввести понятие полосы пропускания: это диапазон частот от 0 до 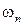 , в котором ошибка воспроизведения гармонического сигнала
, в котором ошибка воспроизведения гармонического сигнала 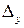 не превышает заданной величины
не превышает заданной величины 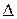 , т.е.
, т.е. 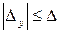 .
.
Так как 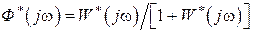 , а
, а 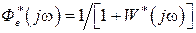 , то для определения
, то для определения 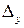 и
и 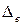 в (1.61) можно использовать АФЧХ разомкнутой системы
в (1.61) можно использовать АФЧХ разомкнутой системы 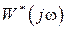 .
.
Если частота входной гармоники достаточно низкая, то несложно показать, что при 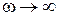
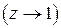 для статических систем
для статических систем 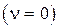
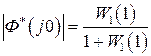 ,
, 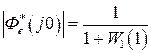 и
и 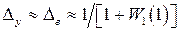 . Для астатических систем
. Для астатических систем 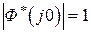 ,
, 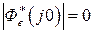 и
и 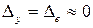 .
.
Таким образом, на точность воспроизведения гармонического сигнала влияет порядок астатизма и коэффициент усиления 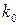 непрерывной части системы, входящей в
непрерывной части системы, входящей в 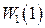 .
.
В заключение отметим, что все изложенное имеет смысл только для устойчивых систем.
Пример 1.9. Рассмотрим импульсную САУ из примеров 1.3 и 1.7. Передаточная функция непрерывной части 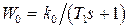 , а передаточная функция разомкнутой импульсной системы
, а передаточная функция разомкнутой импульсной системы 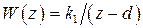 ,
, 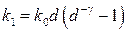 ,
, 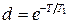 . Рассмотрим случай когда
. Рассмотрим случай когда 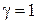 , тогда
, тогда 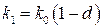 . В примере 1.7 для
. В примере 1.7 для 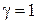 условие устойчивости будет
условие устойчивости будет 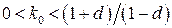 .
.
Найдем 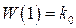 и статическую ошибку
и статическую ошибку
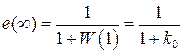 .
.
Из условия устойчивости 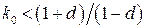 следует, что при любом конечном
следует, что при любом конечном 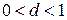 ошибку нельзя сделать меньше величины
ошибку нельзя сделать меньше величины 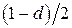 .
.
Оценим ошибки в такой системе при гармоническом воздействии. Очевидно,
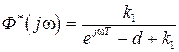 ,
, 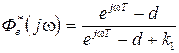 .
.
Примем 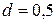 , из условия устойчивости
, из условия устойчивости 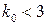 выберем
выберем 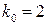 , тогда
, тогда 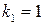 . Модули частотных характеристик будут
. Модули частотных характеристик будут
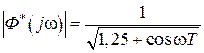 ,
, 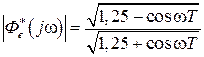 ,
,
Пусть 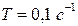 ,
, 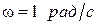 , тогда
, тогда 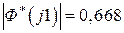 ,
, 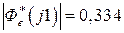 . В соответствии с (1.61) имеем
. В соответствии с (1.61) имеем 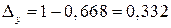 ,
, 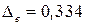 , т.е. ошибки почти совпали. В процентном отношении ошибка составляет 33%.
, т.е. ошибки почти совпали. В процентном отношении ошибка составляет 33%.
Пусть 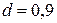 , из условия устойчивости
, из условия устойчивости 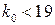 выбираем
выбираем 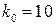 , тогда
, тогда 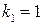 . При
. При 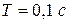 ,
, 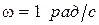 ошибки в этом случае будут
ошибки в этом случае будут 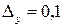 ,
, 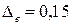 , т.е.
, т.е. 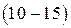 %.
%.
Дата добавления: 2022-02-05; просмотров: 250;











