Кодирование длин серий (Элиас)

Входной поток для кодирования рассматривается как последовательность из нулей и единиц. Идея кодирования заключается в том, чтобы кодировать последовательности одинаковых элементов (например, нулей) как целые числа, указывающие количество элементов в этой последовательности. Последовательность одинаковых элементов называется серией, количество элементов в ней – длиной серии. Например, входную последовательность (общая длина 31бит) можно разбить на серии, а затем закодировать их длины.

000000 1 00000 1 0000000 1 1 00000000 1

Используем, например, γ-код Элиаса. Т.к. в коде нет кодового слова для нуля, то будем кодировать длину серии +1, т.е. последовательность 7 6 8 1 9

7 6 8 1 9 Þ 00111 00110 0001000 1 0001001

Длина полученно й кодовой последовательности равна 25 бит. Метод актуален для кодирования данных, в которых есть длинные последовательности одинаковых бит. В нашем примере, если P(0) >> P(1).

16.3 Алфавитное кодирование

Кодирование F может сопоставлять код всему сообщению из множества S как единому целому или строить код сообщения из кодов его частей. Элементарной частью сообщения является одна буква алфавита А={a₁,a₂,…,a_n}.

Пример 1 А={a₁,a₂,a₃} , B={0,1} a₁ ®1001, a₂ ®0, a₃®010

сообщение a₂a₁a₂a₃ ® 010010010

Пример 2 Азбука Морзе. Входной алфавит – английский. Наиболее часто встречающиеся буквы кодируются более короткими словами:

А ® 01, В ® 1000, С ® 1010, D ® 100, E ® 0, …

Побуквенное кодирование задается таблицей кодовых слов:σ = < α₁® β₁, … , α_n ® β_n>, α_iÎA, β_i ÎB^*.Множество кодовых слов V={β_i} называется множеством элементарных кодов. Побуквенное кодирование пригодно для любого множества сообщений S: F: A^* ®B^*, α_i1 …α_ik=α ÎA^*, F(α)=β_i1…β_ik.

Количество букв в слове α=α₁…α_k называется длиной слова |α| = k. Пустое слово обозначим Λ. Если α=α₁α₂, то α₁ – начало (префикс) слова α, α₂ – окончание (постфикс) слова α.

Побуквенный код называется разделимым (или однозначно декодируемым), если любое сообщение из символов алфавита источника, закодированное этим кодом, может быть однозначно декодировано, т.е. если β_i1 …β_ik = β_j1 …β_jt , то k=t и при любых s=1,…,k i_s=j_s , т.е. любое кодовое слово единственным образом разлагается на элементарные коды. Например, код из первого примера не является разделимым, поскольку кодовое слово 010010 может быть декодируемо двумя способами a₃a₃ или a₂a₁a₂.

Побуквенный код называется префиксным, если в его множестве кодовых слов ни одно слово не является началом другого, т.е. элементарный код одной буквы не является префиксом элементарного кода другой буквы. Например, код из первого примера не является префиксным, поскольку элементарный код буквы a₂ является префиксом элементарного кода буквы a₃.

Утверждение. Префиксный код является разделимым.

Доказательство (от противного). Пусть префиксный код не является разделимым. Тогда существует такая кодовая последовательность β, что она представлена различными способами из элементарных кодов: β=β_i1, …,β_ik = β_j1, …,β_jt (побитовое представление одинаковое) и существует L такое, что при любом S<L следует (β_is= β_js) и (β_it≠ β_jt), т.е. начало каждого из этих представлений имеет одинаковую последовательность элементарных кодов. Уберем эту часть. Тогда β_iL…β_ik = β_jL, …,β_jt, т.е. последовательности элементарных кодов разные и существует β^/, что β_iL=β_jLβ^/ или β_jL=β_iLβ^/ , т.е. β_iL – начало β_jL, или наоборот. Получили противоречие с префиксностью кода.

Заметим, что разделимый код может быть не префиксным.

Пример. Разделимый, но не префиксный код: A={a,b}, B={0,1}, φ = {a®0, b®01}

Приведем основные теоремы побуквенного кодирования.

Теорема (Крафт). Для того, чтобы существовал побуквенный двоичный префиксный код с длинами кодовых слов L₁,…,L_n необходимо и достаточно, чтобы

.

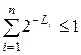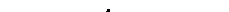Доказательство. Докажем необходимость. Пусть существует префиксный код с длинами L₁,…,L_n. Рассмотрим полное двоичное дерево. Каждая вершина закодирована последовательностью нулей и единиц (как показано на рисунке).

Рисунок 65 Полное двоичное дерево с помеченными вершинами

В этом дереве выделим вершины, соответствующие кодовым словам. Тогда любые два поддерева, соответствующие кодовым вершинам дерева, не пересекаются, т.к. код префиксный. У i-того поддерева на r-том уровне – 2^r-Li вершин. Всего вершин в поддереве 2^r. Тогда , , .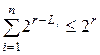

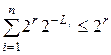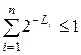Докажем достаточность утверждения. Пусть существует набор длин кодовых слов такой, что 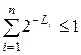. Рассмотрим полное двоичное дерево с помеченными вершинами. Пусть длины кодовых слов упорядочены по возрастанию L₁≤ L₂≤ … ≤ L_n. Выберем в двоичном дереве вершину V₁ на L₁ уровне. Уберем поддерево с корнем в вершине V₁. В оставшемся дереве возьмем вершину V₂ на уровне L₂ и удалим поддерево с корнем в этой вершине и т.д. Последовательности, соответствующие вершинам V₁, V₂,…, V_n образуют префиксный код.

Пример. Построить префиксный код с длинами L₁=1, L₂=2, L₃=2 для алфавита A={a₁,a₂,a₃}. Проверим неравенство Крафта для набора длин 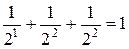. Неравенство выполняется и, следовательно, префиксный код с таким набором длин кодовых слов существует. Рассмотрим полное двоичное дерево с 2³ помеченными вершинами и выберем вершины дерева, как описано выше. Тогда элементарные коды могут быть такими a₁ ®0, a₂®10, a₃ ®11.

Рисунок 66 Построение префиксного кода с заданными длинами

Процесс декодирования выглядит следующим образом. Просматриваем полученное сообщение, двигаясь по дереву. Если попадем в кодовую вершину, то выдаем соответствующую букву и возвращаемся в корень дерева и т.д.

Теорема (МакМиллан). Для того, чтобы существовал побуквенный двоичный разделимый код с длинами кодовых слов L₁,…,L_n , необходимо и достаточно, чтобы .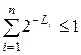

Доказательство. Покажем достаточность. По теореме Крафта существует префиксный код с длинами L₁,…,L_n, и он является разделимым.

Докажем необходимость утверждения. Рассмотрим тождество

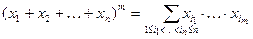
Положим 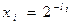. Тогда тождество можно переписать следующим образом

,

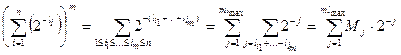где 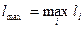, 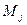– число всевозможных представлений числа j в виде суммы 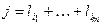. Сопоставим каждому представлению числа j в виде суммы последовательность нулей и единиц длины j по следующему правилу

,

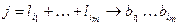где b_s элементарный код длины s. Тогда различным представлениям числа j будут соответствовать различные кодовые слова, поскольку код является разделимым. Таким образом, 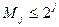и . И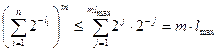спользуя предельный переход получим 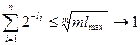при .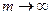

Пример. Азбука Морзе – это схема алфавитного кодирования

A®01, B®1000, C®1010, D®100, E®0, F®0010, G®110, H®0000, I®00, J®0111, K®101, L®0100, M®11, N®10, O®111, P®0110, Q®1101, R®010, S®000, T®1, U®001, V®0001, W®011, X®1001, Y®1011, Z®1100.

Неравенство МакМиллана для азбуки Морзе не выполнено, поскольку

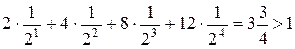
Следовательно, этот код не является разделимым. На самом деле в азбуке Морзе имеются дополнительные элементы – паузы между буквами (и словами), которые позволяют декодировать сообщение. Эти дополнительные элементы определены неформально, поэтому прием и передача сообщений (особенно с высокой скоростью) является некоторым искусством, а не простой технической процедурой.

16.4 Оптимальное алфавитное кодирование

Побуквенное кодирование пригодно для любых сообщений. Однако на практике часто доступна дополнительная информация о вероятностях символов исходного алфавита. С использованием этой информации решается задача оптимального побуквенного кодирования.

Пусть имеется дискретный вероятностный источник, порождающий символы алфавита А={a₁,…,a_n} с вероятностями p_i = p(a_i), 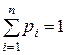. Основной характеристикой источникаявляется его энтропия, которая представляет собой среднее значение количества информации в сообщении источника и определяется выражением (для двоичного случая) . Энтропия характеризует меру неопределенности выбора для данного источника. Например, если А={a₁,a₂}, p₁=0, p₂ =1, т.е. источник может породить только символ a₂, то неопределенности нет, энтропия H(p₁, p₂)=0. Максимальная энтропия будет, если все символы равновероятны, например, А={a₁,a₂}, p₁=1/2, p₂ =1/2, тогда неопределенность максимальная, т.е. H(p₁, p₂)=1.

Для практических применений важно, чтобы коды сообщений имели по возможности наименьшую длину. Основной характеристикой неравномерного кода является количество символов, затрачиваемых на кодирование одного сообщения. Пусть имеется разделимый побуквенный код для источника, порождающего символы алфавита А={a₁,…,a_n} с вероятностями p_i = p(a_i), 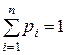, состоящий из n кодовых слов с длинами L₁,…,L_n в алфавите {0,1}. Средней длиной кодового слова называется величина 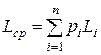или среднее число кодовых букв на одну букву источника.

Пример. Пусть для имеются два источника с одним и тем же алфавитом А={a₁,a₂,a₃} и разными распределениями P₁={1/3, 1/3, 1/3}, P₂={1/4, 1/4, 1/2}, которые кодируются одним и тем же кодом φ = {a₁®10, a₂® 000, a₃® 01}. Средняя длина кодового слова для разных распределений будет различной

L_φ(P₁)=1/3^.2 + 1/3^.3 + 1/3^.2=7/3 ≈2.33

L_φ(P₂)=1/4^.2 + 1/4^.3 + 1/2^.2= 9/4 =2.25

Побуквенный разделимый код называется оптимальным, если средняя длина кодового слова минимальна для данного разделения вероятностей символов. Избыточность кода является показателем качества кода. Избыточностью кода называется разность между средней длиной кодового слова и энтропией источника сообщений r=L_cp-H. Задача эффективного неискажающего сжатия заключается в построении кодов с наименьшей избыточностью, у которых средняя длина кодового слова близка к энтропии источника. К таким кодам относятся классические коды Хаффмена, Шеннона, Фано, Гильберта-Мура.

Приведем некоторые свойства, которыми обладает любой оптимальный побуквенный код.

Лемма 1. Для оптимального кода с длинами кодовых слов L₁,…,L_n: верно соотношение L₁≤L₂≤…≤L_n (p₁≥p₂≥…≥p_n).

Доказательство (от противного): Пусть есть i и j, что L_i>L_j при p_i>p_j. Тогда

L_ip_i+L_jp_j=L_ip_i+L_jp_j+L_ip_j+L_jp_i-L_ip_j-L_jp_i=

=p_i(L_i-L_j)-p_j(L_i-L_j)+L_jp_i+L_ip_j=(p_i-p_j)(L_i-L_j) +L_ip_j+L_jp_i>L_ip_j+L_jp_i,

т.е. если поменяем местами L_i и L_j, то получим код, имеющий меньшую среднюю длину кодового слова. Противоречие с оптимальностью.

Лемма 2 Пусть 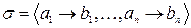схема оптимального префиксного кодирования для распределения вероятностей Р, 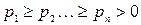. Тогда среди элементарных кодов, имеющих максимальную длину, существуют два, которые различаются только в последнем разряде.

Доказательство. Покажем, что в оптимальной схеме кодирования всегда найдется два кодовых слова максимальной длины. Предположим обратное. Пусть кодовое слово максимальной длины одно и имеет вид 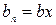, 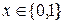. Тогда длина любого элементарного кода не больше длины b, т.е. 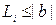, 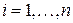. Поскольку схема кодирования префиксная, то кодовые слова 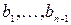не являются префиксом b. С другой стороны, b не является префиксом кодовых слов 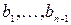. Таким образом, новая схема кодирования 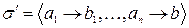также является префиксной, причем с меньшей средней длиной кодового слова 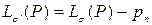, что противоречит оптимальности исходной схемы кодирования. Пусть теперь два кодовых слова 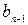и 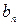максимальной длины отличаются не в последнем разряде, т.е. 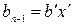, , 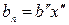, 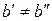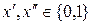. Причем 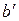, 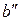не являются префиксами для других кодовых слов 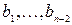и наоборот. Тогда новая схема 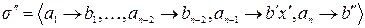также является префиксной, причем 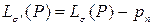, что противоречит оптимальности исходной схемы кодирования.

Рассмотрим алгоритм построения оптимального кода Хаффмена.

1. Упорядочим символы исходного алфавита А={a₁,…,a_n} по убыванию их вероятностей p₁≥p₂≥…≥p_n.

2. Если А={a₁,a₂}, то a₁®0, a₂®1.

3. Если А={a₁,…,a_j,…,a_n} и известны коды <a_j ® b_j >, j = 1,…,n ,то для {a₁,…a_j^/ ,a_j^//…,a_n}, p(a_j)=p(a_j^/)+ p(a_j^//), a_j^/ ® b_j0, a_j^// ®b_j1.

Пример. Пусть дан алфавит A={a₁, a₂, a₃, a₄, a₅, a₆} с вероятностями p₁=0.36, p₂=0.18, p₃=0.18, p₄=0.12, p₅=0.09, p₆=0.07. Будем складывать две наименьшие вероятности и включать суммарную вероятность на соответствующее место в упорядоченном списке вероятностей до тех пор, пока в списке не останется два символа. Тогда закодируем эти два символа 0 и 1. Далее кодовые слова достраиваются, как показано на рисунке 67.

a₁ 0.36 0.36 0.36 0.36 0.64 0

a₂ 0.18 0.18 0.28 0.36 0.36 1

a₃ 0.18 0.18 0.18 0.28 00

a₄ 0.12 0.16 0.18 000 01

a₅ 0.09 0.12 010 001

a₆ 0.07 0100 011

0101

Рисунок 67 Процесс построения кода Хаффмена

Таблица 10 Код Хаффмена

Посчитаем среднюю длину, построенного кода Хаффмена

L_ср(P)=1^.0.36 + 3^.0.18 + 3^.0.18 + 3^.0.12 + 4^.0.09 + 4^.0.07 =2.44,

при этом энтропия данного источника равна

H=-(0.36^.log0.36+2^.0.18^.log0.18+0.12^.log0.12+0.09^.log0.09+0.07log0.07)=2.37

Код Хаффмена обычно строится и хранится в виде двоичного дерева, в листьях которого находятся символы алфавита, а на «ветвях» – 0 или 1. Тогда уникальным кодом символа является путь от корня дерева к этому символу, по которому все 0 и 1 собираются в одну уникальную последовательность.

Рисунок 68 Кодовое дерево для кода Хаффмена