Алгоритм на псевдокоде

Алгоритм А2(Root – указатель на корень дерева,

L, R – левая и правая границы рабочей части массива)

wes=0, summa=0

IF (L<=R)

DO (i=L, L+1, …,R) wes=wes+ V[i].w OD

DO (i=L, L+1,…,R-1)

IF (summa<wes/2 and summa + V[i].w>=wes/2) OD

summa=summa+ V[i].w

OD

Добавление в СДП (Root, V[i])

A2(Root, L, i-1)

A2(Root, i+1, R)

FI

Пример. Рассмотрим процесс построения приближенного ДОП алгоритмом А2 для строки символов из предыдущего примера. Предварительно упорядочим символы по алфавиту.

Таблица 4 Упорядоченный набор вершин

В качестве корня дерева выбираем вершину V₅=К, поскольку

, .

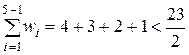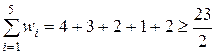Все вершины левее вершины V₅ образуют левое поддерево, вершины правее V₅ – правое поддерево. Далее алгоритм применяется для каждого из поддеревьев в отдельности. Посчитаем средневзвешенную высоту построенного дерева.

P=2^.1+3^.2+3^.2+4^.3+2^.3+2^.3+2^.3+1^.4+1^.4+1^.4+1^.4+1^.5=65

h_ср=65/23=2.82

Рисунок 60 Дерево, построенное приближенным алгоритмом А2

Приведем некоторые свойства рассмотренных приближенных алгоритмов:

1) Сложность алгоритмов как функция от n (количество элементов) зависит следующим образом: время Т = О(n log n), память М = О(n) при n→∞. (Время определяется трудоемкостью сортировки элементов, а память – размером массива для хранения элементов)

2) Дерево, построенное приближенным алгоритмом А1, равносильно случайному (с точки зрения средней высоты) при n→∞, т.е. алгоритм А1– плохой.

3) Дерево, построенное приближенным алгоритмом А2, асимптотически приближается к оптимальному (с точки зрения средней высоты) при n→∞, т.е. алгоритм А2 является хорошим.

4) ИСДП нельзя считать даже приближением к дереву оптимального поиска.

14.4 Варианты заданий

1. Написать процедуру вычисления матрицы весов и матрицы средневзвешенных весов для заданного набора вершин и их весов.

2. Реализовать точный алгоритм построения ДОП.

3. Написать процедуру вычисления средневзвешенной высоты ДОП.

4. Реализовать в виде процедур приближенные алгоритмы построения ДОП.

5. Построить ДОП из 100 чисел с произвольными весами с использованием точного алгоритма. Определить средневзвешенную высоту построенного дерева.

6. Построить почти оптимальные деревья из 100 чисел с использованием приближенных алгоритмов А1 и А2. Сравнить средневзвешенные высоты этих деревьев и ДОП, построенного точным алгоритмом.

7. Построить ДОП ключевых (зарезервированных) слов языка Паскаль (частоты слов определить путем сканирования собственных программ на Паскале).

8. Построить ДОП ключевых (зарезервированных) слов языка Си (частоты слов определить путем сканирования собственных программ на Си).

9. Графически изобразить ДОП из 20 чисел на экране. (Показать значения вершин и их веса).

10. Графически изобразить на экране ДОП ключевых слов языка Паскаль (или Си).

15. Хэширование и поиск

15.1 Понятие хэш-функции

Все рассмотренные ранее алгоритмы были связаны с задачей поиска, которую можно сформулировать следующим образом: задано множество ключей, необходимо так организовать это множество ключей, чтобы поиск элемента с заданным ключом потребовал как можно меньше затрат времени. Поскольку доступ к элементу осуществляется через его адрес в памяти, то задача сводится к определению подходящего отображения H множества ключей K во множество адресов элементов A.

Рисунок 61. Отображение H: K→A

В предыдущих главах такое отображение получалось путем различного размещения ключей (в отсортированном порядке, в виде деревьев поиска), т.е. каждому ключу соответствовал свой адрес в памяти. Теперь рассмотрим задачу построения отображения H: K→A при условии, что количество всевозможных ключей существенно больше количества адресов. Будем обозначать это так: |K| >> |A|. Например, в качестве множества ключей можно взять всевозможные фамилии студентов до 15 букв (|K|= 32¹⁵), а в качестве множества адресов – 100 мест в аудитории (|A|=100). Функция H: K→A, определенная на конечном множестве K, называется хэш-функцией, если |K| >> |A|. Таким образом, хэш-функция допускает, что нескольким ключам может соответствовать один адрес. Хэширование – один из способов поиска элементов по ключу, при этом над ключом k производят некоторые арифметические действия и получают значение функции h=H(k), которое указывает адрес, где хранится ключ k и связанная с ним информация. Если найдутся ключи k_i ≠ k_j, для которых H(k_i)=H(k_j), т.е. несколько ключей отображаются в один адрес, то такая ситуация называется коллизией (конфликтом).

Если данные организованы как обычный массив, то H – отображение ключей в индексы массива. Процесс поиска происходит следующим образом:

1) для ключа k вычисляем индекс h=H(k)

2) проверяем, действительно ли h определяет в массиве T элемент с ключом k, т. е. верно ли соотношение T[H(k)].data = k. Если равенство верно, то элемент найден. Если неверно, то возникла коллизия.

Для эффективной реализации поиска с помощью хэш-функций необходимо определить какого вида функцию H нужно использовать и что делать в случае коллизии (конфликта). Хорошая хэш-функция должна удовлетворять двум условиям:

1) её вычисление должно быть очень быстрым

2) она должна минимизировать число коллизий, т.е. как можно равномернее распределять ключи по всему диапазону индекса.

Для разрешения коллизий нужно использовать какой-нибудь способ, указывающий альтернативное местоположение искомого элемента. Выбор хэш-функции и выбор метода разрешения коллизий – два независимых решения.

Функции, дающие неповторяющиеся значения, достаточно редки даже в случае довольно большой таблицы. Например, знаменитый парадокс дней рождений утверждает, что если в комнате присутствует не менее 23 человек, имеется хороший шанс, что у двух из них совпадет день рождения. Т.е., если мы выбираем функцию, отображающую 23 ключа в таблицу из 365 элементов, то с вероятностью 0,4927 все ключи попадут в разные места.

Теоретически невозможно так определить хэш-функцию, чтобы она создавала случайные данные из неслучайных реальных ключей. Но на практике нетрудно сделать достаточно хорошую имитацию случайности, используя простые арифметические действия.

Будем предполагать, что хэш-функция имеет не более m различных значений: 0≤H(k)<m для любого значения ключа. Например, если ключи десятичные, то возможен следующий способ. Пусть m=1000, в качестве H(k) можно взять три цифры из середины двадцатизначного произведения k•k. Этот метод «середины квадрата», казалось бы, должен давать довольно равномерное распределение между 000 и 999. но на практике такой метод не плох, если ключи не содержат много левых или правых нулей подряд.

Исследования выявили хорошую работу двух типов хэш-функций: один основан на умножении, другой на делении.

1) метод деления особенно прост: используется остаток от деления на m H(K)=K mod m. При этом желательно m брать простым числом.

2) метод умножения H(K)=2^m(A∙K mod w), где A и w взаимно простые числа.

Далее будем использовать функцию H(k)=ORD(k) mod m, где ORD(k) – порядковый номер ключа, m – размер массива (таблицы), причем m рекомендуется брать простым числом.

Если ключ поиска является строкой, то для вычисления ее хэш-номера будем рассматривать её как большое целое число, записанное в 256-ичной системе счисления (каждый символ строки является цифрой), т.е.

H(S₁S₂S₃…S_t)=(S₁∙256^t-1+S₂∙256^t-2+…+S_t-1 256+S_t) mod m .

Используя свойства остатка от деления можно легко вычислить подобные выражения: (a+b)∙mod m=(a mod m + b mod m) mod m. Например, (47+56) mod 10 = (7+6) mod 10 = 3