Алгоритм на псевдокоде

Построение оптимального кода Хаффмена (n,P)

Обозначим

n – количество символов исходного алфавита

P – массив вероятностей, упорядоченных по убыванию

C – матрица элементарных кодов

L – массив длин кодовых слов

Huffman(n,P)

IF (n=2) C[1,1]:=0, L[1]:=1

C[2,1]:=1, L[2]:=1

ELSE q:=P[n-1]+P[n]

j:=Up(n,q) <поиск и вставка суммы>

Huffman(n-1,P)

Down(n,j) <достраивание кодов>

FI

Функция Up (n,q) находит в массиве P место, куда вставить число q и вставляет его, сдвигая вниз остальные элементы.

DO (i=n-1, n-2,…,2)

IF (P[i-1]≤q) P[i]:=P[i-1]

ELSE j:=I

OD

FI

OD

P[j]:=q

Процедура Down (n,j) формирует кодовые слова.

S:=C[j,*] <запоминание j-той строки матрицы элементарных кодов в массив S>

L:=L[j]

DO (i=j,…,n-2)

C[i,*]:=C[i+1,*] <сдвиг вверх строк матрицы С>

L[i]:=L[i+1]

OD

C[n-1,*]:= S, C[n,*]:= S <восстановление префикса кодовых слов из массива S >

C[n-1,L+1]:=0, C[n,L+1]:=1

L[n-1]:=L+1, L[n]:=L+1

16.5 Почти оптимальное алфавитное кодирование

Рассмотрим несколько классических побуквенных кодов, у которых средняя длина кодового слова близка к оптимальной. Пусть имеется дискретный вероятностный источник, порождающий символы алфавита А={a₁,…,a_n} с вероятностями p_i = p(a_i), .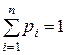

Код Шеннона

Код Шеннонапозволяет построить почти оптимальный код с длинами кодовых слов L_i < - log p_i +1. Тогда L_cp <H(p₁, …,p_n)+1. Код Шеннона строится следующим образом.

1. Упорядочим символы исходного алфавита А={a₁,a₂,…,a_n} по убыванию их вероятностей: p₁≥p₂≥p₃≥…≥p_n.

2. Составим нарастающие суммы вероятностей Q_i:

Q₀=0, Q₁=p₁, Q₂=p₁+p₂, Q₃=p₁+p₂+p₃, … , Q_n=1.

3. Представим Q_i в двоичной системе счисления и возьмем в качестве кодового слова первые é- log₂p_iù знаков после запятой .

Для вероятностей, представленных в виде десятичных дробей, удобно определить длину кодового слова L_i из соотношения

, .

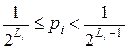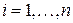Пример.Пусть дан алфавит A={a₁, a₂, a₃, a₄, a₅, a₆} с вероятностями p₁=0.36, p₂=0.18, p₃=0.18, p₄=0.12, p₅=0.09, p₆=0.07. Построенный код приведен в таблице.

Таблица 11 Код Шеннона

Построенный код является префиксным. Вычислим среднюю длину кодового слова и сравним ее с энтропией. Значение энтропии вычислено при построении кода Хаффмена (H = 2.37).

L_ср= 0.36^.2+(0.18+0.18)^.3+(0.12+0.09+0.07)^.4=2.92< 2.37+1