Алгоритм на псевдокоде

Алгоритм А1(Root – указатель на корень дерева)

Обозначим

V.use – логическая переменная в структуре вершины дерева, которая показывает, что данная вершина была использована при построении дерева;

V.w – вес вершины.

Root : = NIL

DO (i = 1,...,n)

V[i].use = ЛОЖЬ

DO (i = 1,...,n)

max:=0, Index:=0

DO (j = 1,...,n)

IF (V[j].w > max и V[j]. use=ЛОЖЬ)

max:=V[j].w

Index:=j

V [index].use :=ИСТИНА

Добавление в СДП (Root, V[index])

Рассмотрим пример построения дерева почти оптимального поиска для символов строки К У Р А П О В А Е Л Е Н А В И К Т О Р О В Н А. Всего символов в строке 23, т.е. W=23. Различные символы определяют различные вершины дерева. Частоты вхождения символов (веса) приведены в таблице.

Таблица 3 Частоты вхождения символов в строку

К	У	Р	А	П	О	В	Е	Л	Н	И	Т

Посчитаем средневзвешенную высоту построенного дерева

P=4^.1+3^.2+3^.3+2^.3+2^.4+1^.4+1^.4+2^.5+ +2^.5+1^.5+1^.6+1^.6=78

h_ср=P/W=78/23=3,39

Рисунок 59 Дерево, построенное приближенным алгоритмом А1

Второй алгоритм (А2) использует предварительно упорядоченный набор вершин. В качестве корня выбирается такая вершина, что разность весов левого и правого поддеревьев была минимальна. Для этого путем последовательного суммирования весов определим вершину V_k, для которой справедливы неравенства:

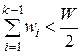и .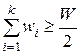

Тогда в качестве "центра тяжести" может быть выбрана вершина V_k, V_k_-1 или V_k₊₁, т. е. вершина, для которой разность весов левого и правого поддерева минимальна. Далее действия повторяются для каждого поддерева