Основные структуры данных
Любая программа в процессе работы обрабатывает некоторые данные. По способу представления в памяти компьютера данные можно разделить на две группы: статические и динамические. Статические данные имеют фиксированную структуру, поэтому размер выделенной для них памяти постоянен. Динамические данные изменяют свою структуру в процессе работы программы, при этом объём памяти изменяется. Основные структуры данных представлены в следующей таблице.
Таблица 1 Различные типы данных
| Статические | Простые | Перечислимые |
| Целые | ||
| Вещественные | ||
| Логические | ||
| Символьные | ||
| Структурированные | Массивы | |
| Записи | ||
| Объединения | ||
| Динамические | Списки | Стек |
| Очередь | ||
| Деревья | АВЛ-деревья | |
| Б-деревья |
Основной характеристикой данных в программировании является тип данных. Любая константа, переменная, выражение, функция всегда относятся к определенному типу. Тип характеризует множество значений, которые может принимать переменная. К простым типам языка программирования относятся целые, вещественные, логические, символьные. Целые типы в языках программирования различаются количеством байт, отведённых в памяти (диапазоном значений) и наличием знака. Вещественные типы характеризуются точностью представления числа. Перечислимые типы образуются в процессе перечисления всех возможных значений. Логический тип является частным случаем перечислимого типа с двумя возможными значениями ИСТИНА и ЛОЖЬ.
Структурированные (составные) типы отличаются от простых тем, что состоят из набора компонент одинакового или разного типа. К структурированным типам относят массивы, записи (структуры), объединения (записи с вариантами).
Массивы – это наиболее известная и распространённая структура данных. Массив представляет собой фиксированное количество элементов одного типа. Всем элементам присваивается одно имя, а к отдельному элементу обращаются по его номеру (индексу). Тип элементов массива может быть любым, но тип индексов должен быть скалярным. Массив – структура данных со случайным (прямым) доступом, т.е. в любой момент времени доступен любой элемент массива, при этом индекс элемента можно вычислять. Обычный способ работы с массивом – выбор определённых элементов и их изменение. Также часто используется перебор элементов в цикле. В памяти элементы массива располагаются последовательно, без разрывов, по возрастанию адресов памяти.
Другой вид структурированных типов – запись состоит из фиксированногочисла компонент называемых полями, которые в отличие от элементов массива могут быть разных типов. Запись также является структурой данных со случайным доступом.
Объединения или (записи с вариантами) используются для размещения в одной и той же области памяти данных различного типа. В один и тот же момент времени в памяти находятся данные только одного типа.
Динамические структуры данных позволяют работать с большими объемами данных. Наиболее используемые динамические структуры данных – списки и деревья.
1.1 Задача сортировки массивов
Пусть дан массив А=(а1, а2, …, аn) и для всех его элементов определены операции отношения: меньше, больше, равно (<, >, =). Необходимо отсортировать массив, т.е. переставить элементы массива А таким образом, что выполняется одно из следующих неравенств:
a1 ≤ а2 ≤ а3 ≤ … ≤ аn
a1 ≥ a2 ≥ a3 ≥ ... ≥ an
Если выполняется первое неравенство, то массив сортируется по возрастанию и такой порядок элементов будем называть прямым. Если выполняется второе неравенство, то массив отсортирован по убыванию и такой порядок элементов будем называть обратным. В дальнейшем, если не оговорено особо, используется прямой порядок сортировки.
При сортировке массивов элементов со сложной структурой возникает задача определить отношение порядка между элементами. Та часть информации, которая учитывается при определении отношения порядка называется ключомсортировки.
Сортировка называется устойчивой, если после её проведения в массиве не меняется относительный порядок элементов с одинаковыми ключами.
Для проверки правильности сортировки массива могут использоваться следующие приемы. Вычисление контрольной суммы элементов массива до и после сортировки дает возможность проверить потерю элементов массива во время процесса сортировки. Определение количества серий элементов массива, т.е. неубывающих последовательностей из элементов массива, позволяет проверить правильность упорядочивания массива, поскольку массив, отсортированный по возрастанию, состоит из одной серии, а в массиве, отсортированном по убыванию, количество серий равно количеству элементов в массиве.
1.2 Трудоемкость методов сортировки массивов
Существует много способов или методов сортировки массивов. Для того, чтобы оценить насколько один метод сортировки лучше другого необходимо каким-то образом оценивать эффективность метода сортировки. Естественно отличать методы сортировки по времени, затрачиваемому на реализацию сортировки. Для сортировок основными считаются две операции: операция сравнения элементов и операция пересылки элемента. Будем считать, что в единицу времени выполняется одна операция сравнения или пересылки. Таким образом, время или трудоемкость метода имеет две составляющие М и С, где
M – количество операций пересылки.
C– количество операций сравнения.
Нетрудно видеть, что M и C – зависят от количества элементов в массиве, т.е. являются функциями от длины массива. Часто бывает трудно определить точное выражение для трудоемкости алгоритма. В этом случае пользуются асимптотической оценкой времени работы.
Будем говорить, что функция g(x) асимптотически доминирует на f(x) или g(x)=O(f(x)), если |g(x)|≤const|f(x)| при x→ ∞. В дальнейшем будем рассматривать асимптотическое поведение величин М и С в зависимости от числа элементов в массиве n, при n→ ∞.
Для функций f, f1, f2 и константы k справедливы свойства:
1. f = O(f)
2. O(k*f) = O(f)
3. O(f1+f2) = O(f1) +O(f2)
Пример.T = 10n + 20
T = O(10n+20) = O(10n) + O(20) = O(n) +O(1) = O(n), при n→ ∞.
Приведем ряд доминирования основных функций
O(1)<O(log n)<O(n)<O(n log n)<O(na)<O(an)<O(n!)<O(nn), при n→ ∞, a>1
Поскольку для различных массивов один и тот же метод сортировки может иметь различную трудоемкость, то необходимо знать в каких пределах могут изменяться величины характеризующие трудоемкость, т.е. определить минимальное и максимальное значения трудоемкости и массивы, на которых достигаются эти значения, а также средние значения величин М и С.
1.3 Задача сортировки последовательностей
Пусть дана последовательность S=S1S2 …Sn , т.е. совокупность данных с последовательным доступом к элементам. Примерами такой последовательности могут служить файл на магнитной ленте, линейный список:
Необходимо переставить элементы последовательности так, чтобы выполнялись неравенства:S1≤ S2 ≤ … ≤ Sn Последовательный доступ означает, что любой элемент списка может быть получен только путём просмотра предыдущих элементов, причём просмотр возможен только в одном направлении. Это является существенным ограничением по сравнению с массивом, где можно было обратиться к любому элементу массиву, используя индекс. Поэтому методы сортировки, разработанные специально для массивов, не годятся для последовательностей, в то время как методы сортировки последовательностей используются и для сортировки массивов. Трудоемкость методов сортировки последовательностей измеряется количеством операций, затрачиваемых на сортировку. Характерными операциями при сортировке последовательностей являются операция сравнения элементов и операция пересылки элемента одной последовательности в другую. Как и прежде будем обозначать количества операций сравнения и пересылки С и М соответственно.
1.4 Теорема о сложности сортировки
При изучении различных методов сортировок возникает закономерный вопрос о построении метода сортировки с минимально возможной трудоемкостью. Следующая теорема устанавливает нижнюю границу трудоемкости для сортировки массива из n элементов.
Теорема. Если все перестановки из n элементов равновероятны, то любое дерево решений, сортирующее последовательность из n элементов имеет среднюю высоту не менее log(n!).
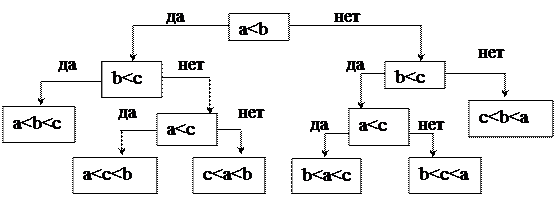 Приведем нестрогое доказательство. Рассмотрим дерево решений для трех элементов a, b, c.
Приведем нестрогое доказательство. Рассмотрим дерево решений для трех элементов a, b, c.
Рисунок 1 Дерево решений для 6 элементов
Все возможные перестановки – это листья дерева (6 вариантов). Чтобы получить конкретную перестановку нужно сделать два или три сравнения. Оценим среднее количество сравнений, необходимых для упорядочивания массива или срденюю длину пути от корня дерева до листьев. Для этого посчитаем сумму длин всевозможных путей от корня до листьев (длина внешнего пути двоичного дерева) и поделим ее на количество листьев Сср= (2+3+3+3+3+2)/6=2,6.
Из теории графов известно, что длина внешнего пути двоичного дерева с m листьями D(m)≥m log m. Поскольку в общем случае на дереве имеется n! листьев. Тогда Сср≥n! log(n!)/n!=lоg n! > n log n–n log e. Последнее неравенство является известной нижней оценкой для значения факториала. Таким образом, не существует алгоритма сортировки n элементов, использующего в среднем меньше чем (n log n – log e) операций сравнения. Класс сложности n log n является предельно достижимым для алгоритмов сортировки с использованием операций сравнения. Что касается количества пересылок, то если мы определим требуемую перестановку, и имеем память для второй копии массива, то достаточно сделать n пересылок. На сегодняшний день алгоритм, требующий nlogn сравнений и n пересылок, неизвестен.
1.5 Задача поиска элементов с заданным ключом
Пусть имеется массив A = (a1, a2, … an) и задан ключ поиска X. Необходимо найти элемент (элементы) массива с ключом X, или определить, что элемента с заданным ключом в массиве нет. Если массив не упорядочен, то единственный путь поиска – просмотр всех элементов массива (линейный поиск) до тех пор, пока не будет найден этот элемент, или просмотрен весь массив. Трудоёмкость поиска в этом случае равна O(n), n→ ∞. Более эффективные алгоритмы поиска можно построить, если предполагать, что массив отсортирован, т.е. a1≤ a2 ≤ a3 ≤ … ≤ an. Трудоемкость метода поиска будем оценивать по количеству сравнений, требуемых для поиска нужного элемента, при этом нас интересует только асимптотическая оценка трудоемкости.
2. Методы сортировки с квадратичной трудоемкостью
2.1 Метод прямого выбора
Один из самых простых методов сортировки, метод прямого выбора, заключается в следующем. Находим наименьший элемент массива и обмениваем его с первым элементом массива. Таким образом, первый элемент можно больше не рассматривать. Среди оставшихся элементов находим наименьший элемент и обмениваем его со вторым элементом массива. Среди оставшихся элементов находим наименьший и переставляем его на третье место и т. д.
Пример.Упорядочим слово методом прямого выбора.
Условные обозначения
Х сравнение элемента Х с текущим максимальным элементом
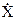 текущий максимальный элемент
текущий максимальный элемент
 Перестановка элементов
Перестановка элементов
| • | • | ||||||
| К | У | Р | А | П | О | В | А |

| |||||||
| • | • | • | • | • | |||
| А | У | Р | К | П | О | В | А |

| |||||||
| • | • | • | |||||
| А | А | Р | К | П | О | В | У |

| |||||||
| • | |||||||
| А | А | В | К | П | О | Р | У |

| |||||||
| • | • | ||||||
| А | А | В | К | П | О | Р | У |

| |||||||
| • | |||||||
| А | А | В | К | О | П | Р | У |

| |||||||
| • | |||||||
 А А
| А | В | К | О | П | Р | У |
| А | А | В | К | О | П | Р | У |
Рисунок 2 Метод прямого выбора
Дата добавления: 2022-02-05; просмотров: 493;











