Конические зубчатые передачи.

Конической называется зубчатая передача, предназначенная для передачи и преобразования вращательного движения между звеньями, оси вращения которых пересекаются.

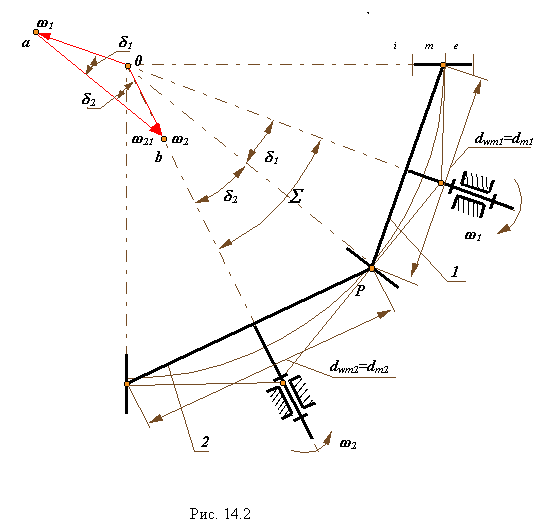
Схема конической передачи представлена на рис. 14.2. Оси колес зубчатой передачи пересекаются в точке 0. Угол∑между осями колес ( или между векторами угловых скоростей звеньев w1 и w2 ) называется межосевым углом. Этот угол может изменяться в пределах 0° < ∑ < 180°. При ∑= 0° передача превращается в цилиндрическую с внешним зацеплением, а при ∑= 180° - в цилиндрическую с внутренним зацеплением. Таким образом, коническая передача является общим случаем зубчатой передачи, нежели цилиндрические. Начальные или аксоидные поверхности в конической передаче имеют форму конусов. Аксоидными называются поверхности, которые образуются осями мгновенного относительного вращения колес, в системах координат связанных с колесами ( звеньями передачи ). Если колеса передачи обработаны без смещения исходного контура, то аксоидные поверхности совпадают с делительными. При относительном движении аксоиды перекатываются друг по другу, при этом скольжение возможно только в направлении оси относительного вращения. Поэтому вектора угловых скоростей звеньев связаны между собой векторным уравнением

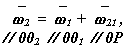
если известна величина w1, то из этого уравнения можно определитьw1 и w2. Из векторного треугольника ∆ a0b

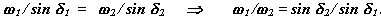
Передаточное отношение конической передачи

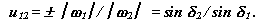
Так как 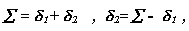тo

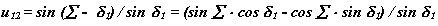
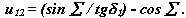
Тогда углы начальных ( делительных при х=0 ) конусов

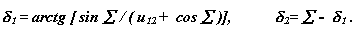
Геометрия зацепления в конической зубчатой передаче:

Как и в цилиндрических, так и в конических зубчатых передачах наиболее часто применяют эвольвентное зацепление. Эвольвентная поверхность зуба конического колеса образуется при перекатывании производящей плоскости по основному конусу. Эвольвентные кривые формируются на соосных сферических поверхностях с центром в вершине основного конуса. Поэтому для расчета геометрии эвольвентной конической передачи необходимо применять сферическую геометрию. Так как это сложно, то используют приближенный метод расчета геометрии - метод дополнительных конусов, предложенный английским столяром Томасом Тредгольдом. При этом методе расчет геометрии проводится для эквивалентного цилиндрического зацепления двух секторов. Эти сектора образуются развертками конусов, которые построены на внешней сфере радиуса R we . Радиусы оснований этих конусов r we1 = r e1 и r we2 = r e2, а образующие являются касательными к сфере (рис.14.3). Числа зубьев колес эквивалентного цилиндрического зацепления рассчитываются на основании следующих формул

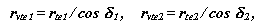
где rte1и rte2 - радиусы торцевых делительных окружностей на внешней сфере, rvte1 и rvte2- радиусы делительных окружностей эквивалентного цилиндрического зацепления.

Так как 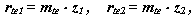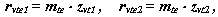то :

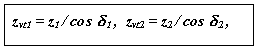
где z1 и z2 - числа зубьев колес конической передачи, zvt1 и zvt2 - числа зубьев колес эквивалентного цилиндрического расчетного зацепления ( эти величины могут быть дробными).

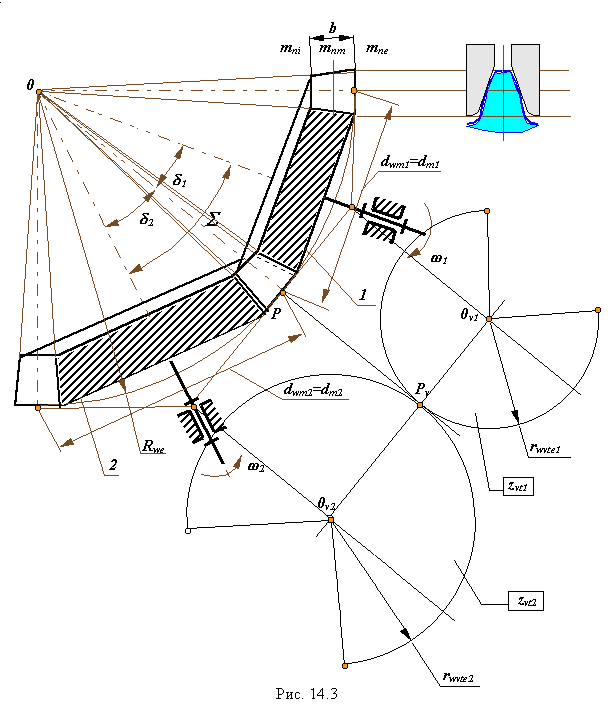
После определения чисел зубьев эквивалентного цилиндрического зацепления, приближенный расчет геометрических параметров для внешнего торца конического зацепления можно проводить по рассмотренным выше формулам цилиндрического эвольвентного зацепления. Радиус внешней сферы (длина образующей начального или делительного конуса)

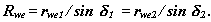
Ширина зубчатого венца 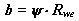, где b=0.3....0.4 - коэффициент ширины зубчатого венца.

По форме линии зуба конические зубчатые передачи различаются на: прямозубые; косозубые; с круговым зубом; с эвольвентной линией зуба; с циклоидальной линией зуба.