Преобразование Лапласа как метод анализа линейных схем
В рамках настоящего пособия «Основы схемотехники дискретно-аналоговых ИМС» рассматриваются схемотехника и методы исследования линейных КМДП дискретно-аналоговых интегральных схем. Как известно, все множество параметров линейной схемы по определению не зависит от уровня (величины, амплитуды) входного по отношению к схеме сигнала 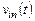 . По этой причине взаимосвязь входного
. По этой причине взаимосвязь входного 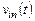 и выходного
и выходного 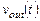 сигналов может быть выражена линейной функцией.
сигналов может быть выражена линейной функцией.
Если сигналы рассматриваются во временной области, то используется импульсная характеристика (функция) в сочетании с интегралом Дюамеля («свертки»). Если известны входной сигнал 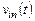 и импульсная характеристика
и импульсная характеристика 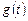 линейной схемы, то сигнал
линейной схемы, то сигнал 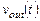 на выходе схемы определяется из следующего выражения [1 – 4]:
на выходе схемы определяется из следующего выражения [1 – 4]:
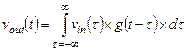 (1.1)
(1.1)
Другим общепризнанным методом анализа линейных схем является спектральный метод . В рамках этого метода в теории связи наибольшее распространение получил метод преобразование Лапласа [1 – 4], которое:
– в отличие от преобразования Фурье, не ограничено использованием только сигналов, описываемых абсолютно интегрируемыми функциями;
– позволяет решать линейные интегро-дифференциальные уравнения методами алгебры;
– в отличие от анализа во временнòй области позволяет не только описывать нестационарные (переходные) процессы, но также получать и анализировать стационарные амплитудно-частотные и фазочастотные особенности.
Исчерпывающей характеристикой линейной схемы в спектральном методе является передаточная функция 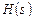 , специфическая для каждой системы. При подаче на вход линейной системы сигнала
, специфическая для каждой системы. При подаче на вход линейной системы сигнала 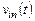 , сигнал
, сигнал 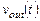 на выходе находится следующим образом:
на выходе находится следующим образом:
(А) определяется ИЗОБРАЖЕНИЕ 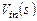 входного сигнала
входного сигнала 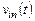 на комплексной плоскости
на комплексной плоскости 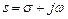 :
:
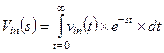 (1.2)
(1.2)
(В) изображение входного сигнала 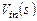 умножается на передаточную функцию
умножается на передаточную функцию 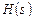 системы, в результате чего получается изображение
системы, в результате чего получается изображение 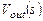 сигнала на выходе линейной системы:
сигнала на выходе линейной системы:
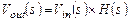 (1.3)
(1.3)
(С) из изображения 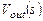 сигнала на выходе определяется ОРИГИНАЛ
сигнала на выходе определяется ОРИГИНАЛ 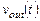 выходного сигнала:
выходного сигнала:
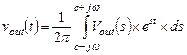 (1.4)
(1.4)
Интегрирование в выражении (1.4) производится в комплексной плоскости 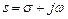 вдоль прямой, проходящей параллельно мнимой оси на расстоянии
вдоль прямой, проходящей параллельно мнимой оси на расстоянии 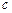 от последней и замыкается вдоль дуги бесконечно большого радиуса, образовывая замкнутый контур интегрирования. При этом внутри контура должны находиться все полюсы подынтегральной функции, и значение
от последней и замыкается вдоль дуги бесконечно большого радиуса, образовывая замкнутый контур интегрирования. При этом внутри контура должны находиться все полюсы подынтегральной функции, и значение  в этом случае равно сумме вычетов в полюсах подынтегральной функции.
в этом случае равно сумме вычетов в полюсах подынтегральной функции.
При подаче сигнала на вход системы вначале возникает нестационарный процесс установления нового состояния (переходной процесс), и действительная часть 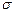 комплексной переменной
комплексной переменной 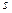 входит в показатели экспонент, определяющих затухающий (при
входит в показатели экспонент, определяющих затухающий (при 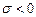 ) или возрастающий (при
) или возрастающий (при 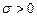 ) характер переходного процесса. После затухания переходного процесса система либо остается в покое, либо остаются только вынужденные процессы (как правило, колебания), обусловленные колебаниями входного сигнала. Если следы нестационарности процесса исчезли, можно считать, что во все последующее время
) характер переходного процесса. После затухания переходного процесса система либо остается в покое, либо остаются только вынужденные процессы (как правило, колебания), обусловленные колебаниями входного сигнала. Если следы нестационарности процесса исчезли, можно считать, что во все последующее время 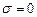 , и
, и 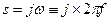 . В этом случае (в новом стационарном состоянии) выражения (1.2) – (1.4) представляют собой преобразования Фурье, являющемся частным случаем преобразования Лапласа. Модуль полученного комплексного выражения представляет зависимость от частоты модуля коэффициента передачи (усиления) системы, а фаза представляет зависимость от частоты фазы входного синусоидального сигнала.
. В этом случае (в новом стационарном состоянии) выражения (1.2) – (1.4) представляют собой преобразования Фурье, являющемся частным случаем преобразования Лапласа. Модуль полученного комплексного выражения представляет зависимость от частоты модуля коэффициента передачи (усиления) системы, а фаза представляет зависимость от частоты фазы входного синусоидального сигнала.
Основные свойства преобразования Лапласа
Пусть функция 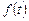 является оригиналом, а
является оригиналом, а 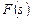 – изображением функции
– изображением функции 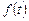 , т.е.
, т.е. 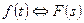 . Тогда из (1.2) – (1.4) можно получить основные свойства преобразования Лапласа.
. Тогда из (1.2) – (1.4) можно получить основные свойства преобразования Лапласа.
Таблица 1.1
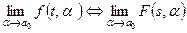
| 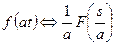
|
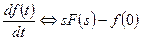
| 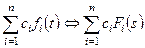
|
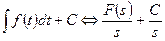
| 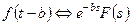
|
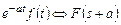
| 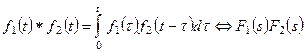
|
Таблица некоторых преобразований Лапласа
Таблица 1.2
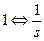
| 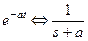
| 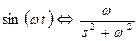
|
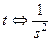
| 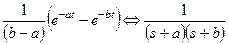
| 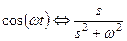
|
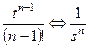
| 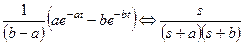
| 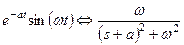
|
Дата добавления: 2022-02-05; просмотров: 407;











