Схемы деления целых чисел без знака
В ЭВМ деление целых чисел – это целочисленное деление с получением частного и остатка. В большинстве ЭВМ имеется две команды деления целых чисел: DIV (деление чисел без знака) и IDIV (деление чисел со знаком).
При выполнении команды IDIV остатку приписывается знак делимого. Например, при делении числа (–5) на (–2) в частном получается 2 и (–1) в остатке.
Деление в ЭВМ обычно сводится к выполнению последовательности вычитания делителя сначала из делимого, а затем из образующихся частичных остатков и сдвига частичных остатков.
Деление производится методом подбора цифр частного (цифра за цифрой). Классический метод подбора цифр частного (начиная со старшей) заключается в сравнении по величине делимого и выровненного делителя. Выравнивание делителя заключается в выравнивании его порядка (веса его старшего разряда) до порядка делимого. Если делимое или частичный остаток оказывается равным или меньшим большим ? делителя, то производится вычитание делителя из делимого и в очередном разряде частного фиксируется цифра 1, в противном случае вычитание не производится, и в очередном разряде частного фиксируется цифра 0. В любом случае производится сдвиг делимого на один разряд влево (увеличение порядка делимого) и частного. Этот процесс продолжается до получения всех цифр частного.
Машинное деление реализуется по двум основным схемам:
1. Деление с неподвижным делимым и сдвигаемым вправо делителем.
При делении целых чисел используется делимое двойной разрядности, а делитель одинарной. Частное от деления и остаток получаются одинарной разрядности. Недостатком способа деления с неподвижным делителем делимым является удвоенная разрядность не только регистра делимого, но и сумматора.
2. Устройство деления с сумматором обычной (не удвоенной) разрядности позволяет использовать способ деления со сдвигаемым влево делимым. Это наиболее распространенная схема деления.
Устройство деления со сдвигаемым влево делимым.
Данный способ деления позволяет использовать сумматор обычной (не удвоенной) разрядности Это наиболее распространенная схема деления.
Схема выполнения деления со сдвигаемым делимым представлена
на рис. 5.7.
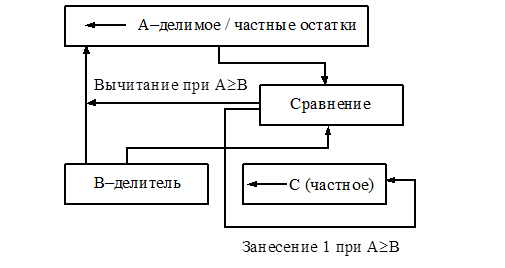
Рис. 5.7. Схема выполнения деления со сдвигаемым делимым
Сравнение чисел можно производить при помощи сумматора с цепями сквозного переноса. Сигнал переноса со старшего разряда сумматора возникает, если вычитаемое меньше или равно уменьшаемому, т.е. совпадает с условием формирования единицы в разряде частного и выполнения операции вычитания.
В случаях использования сумматоров без цепей сквозного переноса сравнение чисел производят при помощи операции вычитания. Но если результат вычитания показывает, что делимое или частный остаток был меньше делителя, то для определения последующих цифр частного необходимо восстанавливать делимое (или частный остаток). Для восстановления отрицательных остатков можно использовать операцию суммирования делителя с отрицательным остатком. Это схема деления с восстановлением отрицательных остатков (рис. 5.5).
При проектировании схем деления следует учитывать следующие особенности операции деления:
· При делении 2n-разрядного делимого на n-разрядный делитель возможно получение (n+1)-разрядного частного. Это случай переполнения разрядной сетки. Переполнение разрядной сетки выявляется при первом пробном вычитании. Если результат пробного вычитания дает положительный частный остаток, то это признак переполнения при делении.
· Если пробное вычитание дает отрицательный остаток при правильном выборе разрядной сетки, то это гарантирует отсутствие переполнения, но делимое (после восстановления любым способом) необходимо сдвинуть на один разряд влево. Следовательно в регистре делимого следует предусмотреть дополнительный старший разряд.
Дата добавления: 2022-02-05; просмотров: 675;











