Схемы ускоренного умножения


Схемы ускоренного умножения строятся на основе перехода на системы счисления с большим основанием. Для быстрого преобразования используются системы счисления с основаниями, равными степеням двойки: 4, 8, 16 и т.д. При использовании этих схем приходится использовать таблицы умножения для этих систем. Для быстроты преобразования используют системы счисления с основаниями, равными степеням двух: 4, 8, 16 и т.д. При этом приходится применять таблицы умножения для этих систем счисления. Это табличные методы. Например, нужно построить схему умножения для однобайтных чисел. Для этого нужна таблица в 216 двухбайтных строк (128 Кбайт). В этой таблице нужно разместить результаты перемножения любых двух однобайтных чисел. Адресом служат комбинации байтовых операндов. Результат читается из таблицы. Произведение считывается из таблицы по адресу, которым служит комбинация этих однобайтнах чисел.

Сами таблицы могут быть реализованы на основе комбинационных схем, для которых таблицами истинности являются таблицы умножения. Примером может служить умножитель двух 16-ти разрядных операндов, вырабатывающихй за один такт произведение двойной длины в прямом или обратном коде, в составе микросхем серии КР1802.

Можно использовать и комбинированные решения. Например, при наличии комбинационных схем умножения только на четыре разряда, байты можно разбить на тетрады и каждое байтовое число длиной в один байт представить в виде полинома:

А = а1 24 + а0

B = b1 24 + b0

С = А´B = 28 а1 b1+ 24 a0 b1 + 24 a1 b0 + а0 b0

Для вычисления этого выражения требуется четыре обращения к комбинационным схемам (или одно обращение к четырем комбинационным схемам) с аргументами: а1 b1, a0 b1, a1 b0, а0 b0 и сложение полученных произведений с соответствующими сдвигами на 8, 4, 4, и 0 разрядов влево. В этом решении случае требуется таблица всего на 64 байта, реализованная в виде комбинационной схемы.

Можно обойтись совсем без таблиц при использовании ускоренного умножении со сдвигом множителя на два разряда.

Эта схема умножения применима только при сдвиге множителя вправо (схемы а и b – умножение с младших разрядов).

Особенность схемы ускоренного умножения – это сдвиги множителя на два разряда и действия при формировании частичных произведений. В схеме анализируется комбинация знака суммы частичных произведений и двух двоичных цифр множителя .

Особенностью этой схемы являются действия при формировании частичных произведений, которые выполняются в зависимости от соотношения знака суммы частичных произведений и двух двоичных цифр множителя

Ниже рассматривается пример умножения чисел в прямом коде. Для этого примера комбинации цифр (знак суммы частичных произведений и двух двоичных цифр множителя) соответствуют следующим действиям:

· 0 00 - блокировка прибавления множимого.

· 0 01 - суммирование множимого с суммой частичных произведений.

· 0 10- суммирование сдвинутого на один разряд влево (умноженного на 2) множимого с суммой частичных произведений.

· 0 11 - вычитание значения множимого из суммы частичных произведений. При этом сумма частичных произведений становится отрицательной, так как учетверенное множимое всегда больше суммы частичных произведений. Здесь сложение множимого, умноженного на три, заменяется его вычитанием в текущем цикле, с последующим прибавлением учетверенного множимого. (3=4–1).

· 1 00 - суммирование множимого с суммой частичных произведений.

· 1 01 - суммирование сдвинутого на один разряд влево множимого с суммой частичных произведений.

· 1 10 - вычитание значения множимого из суммы частичных произведений.

· 1 11 - блокировка прибавления множимого.

Блок схема алгоритма умножения со сдвигом на два разряда множителя представлена на рис.5.6.

 

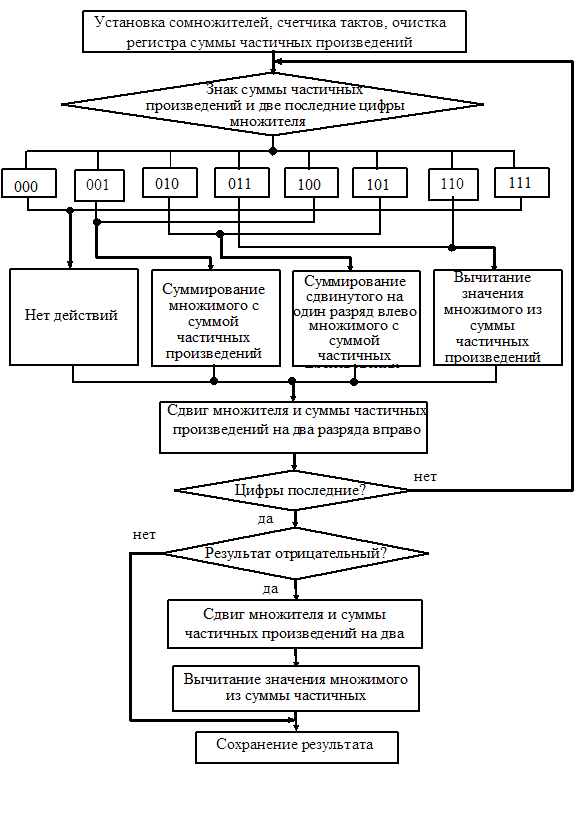
Рис.5.6. Блок схема алгоритма умножения со сдвигом на два разряда множителя

 

При умножении на два разряда возможен случай, когда при умножении на последние цифры производится вычитание. В этих случаях производится дополнительный сдвиг на два разряда суммы частичных произведений вправо или множимого на два разряда влево и сложения и сложение результата с суммой частичных произведений.

Пример: Ускоренное умножения целых чисел без знака по схеме а со сдвигом частичных произведений вправо.

А = +15(10) = 0,1111(2) – множимое.

В = +13(10)= 0,1101(2) – множитель.

С = 0,0000 – сумма частичных произведений.

В примерах примере знак суммы частичных произведений используется для выявления отрицательных остатков (возможен вариант использование фиксации переносов из старших разрядов отрицательные остатки можно также выявлять по факту переноса из старшего разряда). Знак множителя используется только для определения знака произведения и в примере не рассматривается. Вертикальная черта в регистре множителя (В) отделяет разряды частичных произведений от разрядов множителя.

 

 

Множимое А Произведение С Множитель В Комментарии
0,1111 0,0000 ½1101 Исходное состояние
0,0000 00½11 01 Сквозной сдвиг суммы частичных произведений и множителя вправо на два разряда с размножением знака.
0,0000 0,1111 0,1111 00½11 01 Анализ трех бит 001 (знака суммы частичных произведений и двух младших разрядов множителя) и прибавления множимого.
0,0011 11½00 11 Сквозной сдвиг суммы частичных произведений и множителя вправо на два разряда с размножением знака
0,0011 1,0001 1,0100 11½00 11 Анализ трех бит 011 (знака суммы частичных произведений и двух младших разрядов множителя) и вычитание множимого
1,1101 0011½ 00 Дополнительный сквозной сдвиг суммы частичных произведений и множителя вправо на два разряда с размножением знака
1,1101 0,1111 0,1100 0011½ 00 Анализ трех бит 100 (знака суммы частичных произведений и двух младших разрядов множителя) и прибавления множимого.

 

 

Результат С = 0,11000011(2) = 195(10).

Дата добавления: 2022-02-05; просмотров: 408;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.009 сек.