Позиционные системы счисления

Другим классом систем счисления являются позиционные системысчисления. В этих системах счисления для записи (кодирования) количественных значений определяются множества символов (цифр), например: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Числовое значение записи в этой системе зависит не только от совокупности используемых цифр, но и от их взаимного расположения (разрядных позиций или просто разрядов).

Для позиционных систем счисления число символов, определенных для кодирования чисел, называется основанием системы счисления q.

Наименование позиционной системы счисления производится по значению основания системы счисления (десятичная – q=10, двоичная – q = 2).

Любое число N в позиционной системе счисления можно представить в виде сокращенной записи полинома (записываются только коэффициенты степеней основания):

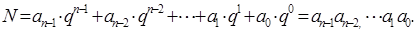
Например, в десятичной системе счисление запись числа N = 134 соответствует сокращенной формой представления полинома:

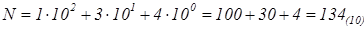
Здесь и далее, при необходимости указания позиционной системы счисления, использованной при кодировании числа, основание системы счисления указывается в виде нижнего индекса в скобках – .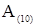

Если значение числа превышает значение основания системы счисления, то запись является многоразрядной. При этом каждый разряд имеет вес, равный соответствующей степени основания системы счисления. В десятичной системе счисления веса разрядов (начиная с младших разрядов) принимают значения единиц, десятков, сотен и т.д. Названия числовых величин соответствуют значению цифр и весам разрядов. Например, число 134 читается как одна сотня, три десятка и 4 единицы или сокращенно – сто тридцать четыре.

Все вышеизложенное применимо и для дробных и для смешанных чисел (неправильных дробей), при этом веса разрядов дробной части являются отрицательными степенями основания системы счисления. Для десятичной системы счисления – это десятые, сотые и т.д. доли единицы.