Дополнительный код.

Кодирование чисел в дополнительном коде можно получить естественным путем при помощи операции вычитания (моделирования работы вычитающего счетчика). Для начала рассмотрим дополнительный код для десятичной системы счисления. За начальное состояние возьмем значение счетчика – 4, разрядность счетчика – 3:

Начальное состояние счетчика: 0 003 положительное число 3

после вычитания 1 0 002 положительное число 2

после вычитания 1 0 001 положительное число 1

после вычитания 1 0 000 нулевое значение счетчика

после вычитания 1 9 999 отрицательное число – минус 1; это и следующие значения рассматриваются как коды отрицательных чисел

после вычитания 1 9 998 отрицательное число – минус 2

после вычитания 1 9 997 отрицательное число – минус 3

и т.д.

Положительные числа от отрицательных отличаются значением старшего разряда. Если он равен 9. то число отрицательное, иначе – положительное.

Пример выполнения вычитания в дополнительном коде:

А = В – С. где: В = 0 005, С = 0 003

Заменяем действие вычитание положительного числа на сложение с отрицательным числом: А = В + ( – С). Здесь по коду положительной величины С (0 003) находится код отрицательной величины ( – С = 9 997) и производится действие сложение:

0 005

+ 9 997

1½0 002

Единица переноса из старшего разряда (отделена вертикальной чертой) в данном случае просто отбрасывается.

Определение кода отрицательной величины по коду положительной величины (операция инверсии знака) производится по правилу: каждую цифру (включая знак) меняют на дополнение до 9: (0® 9), (1®8), (2®7)….(9 ®0) и полученный результат увеличивают на 1.

В десятичной системе счисления дополнительный код не симметричен по отношению к множествам положительных и отрицательных чисел, записываемых в регистр.

Двоичный дополнительный код более симметричен по отношению к множествам положительных и отрицательных чисел (отрицательных чисел записывается больше только на одно число).

Определение кода отрицательной величины по коду положительной величины (приписывание отрицательного знака) производится по правилу: каждую цифру числа (включая знак) меняют на противоположную (ноль на единицу, а единицу на ноль) и полученный результат увеличивают на 1.

Два числа, одинаковых по абсолютной величине, но имеющих разные знаки, являются дополнительными в том смысле, что их сумма равна нулю.

Пример. Числа: А = 5₍₁₀₎= 0.0101₍₂₎ и В = (–5₍₁₀₎)= 1.1011₍₂₎ являются дополнительными, т.к. их сумма равна нулю (перенос из старшего разряда отбрасывается):

0.0101

+ 1.1011

1| 0.0000.

Они содержат значащие цифры и знак (в примере знак отделен точкой).

Имеется и другая интерпретация дополнительного кода. Знаковый разряд рассматривается как обычный цифровой, но с отрицательным весом. У положительных чисел значение этого разряда равно нулю, а у отрицательного – минус единица в соответствующей (положительной) степени.

Так как 2ⁿ > 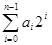, число всегда отрицательно, если его старшая (знаковая) цифра равна 1.

Подсчет значения чисел для предыдущего примера производится следующим образом:

А = 0.0101 = 100₍₂₎ + 1₍₂₎ = 4₍₁₀₎ + 1₍₁₀₎ = 5₍₁₀₎

В = 1.1011 = (– 10000₍₂₎) + 1000₍₂₎ + 10₍₂₎ +1₍₂₎ = (– 16₍₁₀₎) +8₍₁₀₎+2₍₁₀₎+1₍₁₀₎ = (– 5₍₁₀₎).

Такая интерпретация дополнительного кода позволяет проектировать более эффективные алгоритмы микропрограмм арифметических операций.