Перевод целых чисел или целой части неправильной дроби.
Метод деления на основание целевой системы счисления.
Представим исходное число 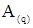 в виде полинома степени p, где p – основание целевой системы счисления, а
в виде полинома степени p, где p – основание целевой системы счисления, а 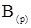 – полином в целевой системе счисления:
– полином в целевой системе счисления:
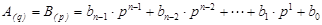 1)
1)
Искомое изображение величины 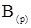 находится как совокупность разрядных цифр:
находится как совокупность разрядных цифр: 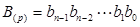 . 2)
. 2)
Для нахождения (разряд за разрядом) разрядных цифр числа 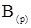 , разделим число в исходной системе счисления
, разделим число в исходной системе счисления 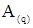 (равенство 1) на основание целевой системы счисления p. В результате этой операции получаем новое равенство:
(равенство 1) на основание целевой системы счисления p. В результате этой операции получаем новое равенство:
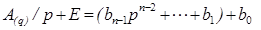 3)
3)
где:
· 
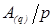 – частное от деления исходного числа на основание целевой системы счисления p,
– частное от деления исходного числа на основание целевой системы счисления p,
· 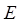 – остаток от деления исходного числа на основание целевой системы счисления p.
– остаток от деления исходного числа на основание целевой системы счисления p.
Из выражения 3 следует:
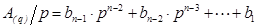 4)
4)
и 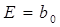 . 5)
. 5)
Таким образом, младшая цифра числа в целевой системе счисления совпадает с остатком от деления числа на основание целевой системы счисления.
Значения остальных цифр числа 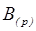 (цифра за цифрой) можно найти, продолжая деление очередных частных на основание p. Деление продолжается, пока очередное частное не станет меньше основания целевой системы счисления.
(цифра за цифрой) можно найти, продолжая деление очередных частных на основание p. Деление продолжается, пока очередное частное не станет меньше основания целевой системы счисления.
Полученные цифры числа в новой системе счисления представлены в исходной системе счисления.
Если перевод производится в систему счисления с большим основанием, то требуется дополнительный перевод каждой цифры в целевую систему счисления.
Пример перевода десятичного числа 43(q = 10) в двоичную систему счисления.
| b0 = 1 | |||||
| b1 = 1 | |||||
| b2 = 0 | |||||
| b3 = 1 | |||||
| b4 = 0 | |||||
| b5 = 1 | |||||
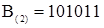
|
Пример обратного перевода двоичного числа  в десятичную систему счисления
в десятичную систему счисления
Деление делается в двоичной системе счисления. Вначале основание целевой системы счисления 10 переводится в двоичную систему счисления:
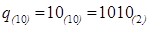
Двоичное число 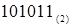 делится на основание целевой системы счисления –
делится на основание целевой системы счисления – 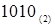 . В результате деления получается частное –
. В результате деления получается частное – 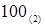 и остаток
и остаток 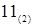 , равный младшей цифре числа в искомой системе счисления. Так как полученное частное –
, равный младшей цифре числа в искомой системе счисления. Так как полученное частное – 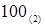 меньше основания
меньше основания 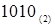 (целевой системы счисления), то оно является старшей цифрой искомого кода.
(целевой системы счисления), то оно является старшей цифрой искомого кода.
Искомый код в двоично-десятичной системе приобретает вид: 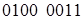 или, после перевода каждой цифры в десятичную систему счисления, –
или, после перевода каждой цифры в десятичную систему счисления, – 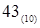 .
.
Дата добавления: 2022-02-05; просмотров: 508;











