Перевод дробных чисел или дробной части неправильной дроби.

Метод последовательного умножения на основание системы счисления.

Представим исходную правильную дробь 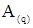в виде полинома степени p, где p – основание, а 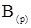– полином целевой системы счисления:

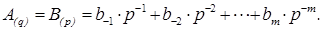5)

Искомое изображение величины 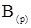находится как совокупность разрядных цифр: 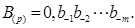. 6)

Для нахождения (разряд за разрядом) разрядных цифр числа 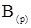, умножим число в исходной системе счисления 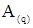(равенство 1) на основание целевой системы счисления p. В результате этой операции получаем неправильную дробь, в которой целая часть b_-1Ÿ p⁰ = b_-1 будет равна первой старшей цифре дроби в целевой системе счисления:

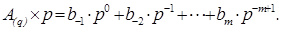7),

где : 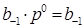-целая часть неправильной дроби и первая цифра дробной части числа в целевой системе счисления.

Продолжая эту операцию над дробной частью ( 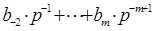) правой части равенства (7) можно цифра за цифрой вычислить значение последующих разрядов дроби.

Если перевод производится в систему счисления с большим основанием, то требуется отдельный перевод каждой цифры в целевую систему счисления.

Пример перевода правильной дроби 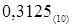в двоичную систему счисления.

Сдвиг переносов на 1 позицию	Умножение дробной части на основание – 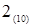. (Умножение производится в десятичной системе счисления.)
0,	,3125 ´ 2
0,0	,6250 ´ 2
0,01	,2500 ´ 2
0,010	,5000 ´ 2
0,0101	,0000 ´ 2
Результат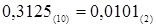

Пример перевода числа 0,0101(2) в десятичную систему счисления.
Сдвиг переносов на 4 позиции	Умножение дробной части на основание – 10(10) = 1010(2)
0,	,0101 ´ 1010 = 0011,0010
0,0011	,0010 ´ 1010 = 0001,0100
0,0011 0001	,0100 ´ 1010 = 0010,1000
0,0011 0001 0010	,1000 ´ 1010 = 0101,0000
0.0011 0001 0010 0101	,0000
Результат =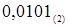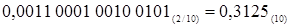

В общем случае, дробные числа переводятся из одной системы счисления в другую приближенно, так как дробная часть числа при последовательном умножении на основание целевой системы счисления может не принимать значения нуля. В таких случаях перевод продолжается до достижения заданной точности. Примером может служить перевод числа 0,3₍₁₀₎ в двоичную систему счисления

Сдвиг переносов на 1 позицию	Умножение дробной части на основание – 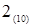. (Умножение производится в десятичной системе счисления.)
0,	,3 ´ 2
0,0	,6 ´ 2
0,01	,2 ´ 2
0,010	,4 ´ 2
0,0100	,8 ´ 2
0,01001	,6 ´ 2 и т.д.
Результат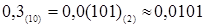

Рассмотренные выше методы перевода чисел из одной позиционной системы счисления в другую позиционную систему счисления являются классическими, но не единственными. На практике могут применяться и другие методы, например, метод подбора суммы убывающих степеней основания целевой системы счисления, равной по величине числу в исходной системы счисления. Например, число 138₍₁₀₎, может быть представлено в виде суммы степеней числа 2: 138₍₁₀₎ = 128₍₁₀₎ + 8₍₁₀₎ + 2₍₁₀₎ = 1´2⁽⁷⁾ + 0´2⁽⁶⁾ + 0´2⁽⁵⁾ + 0´2⁽⁴⁾ + 1´2⁽³⁾ + 0´2⁽²⁾ + 1´2⁽¹⁾ + 0´2⁽⁶⁾ = 10001010.