Примеры анализа алогритмов

Пример 1. Рассмотрим задачу поиска наибольшего элемента в списке из n чисел. Для простоты предположим, что этот список реализован в виде массива. Ниже приведен псевдокод алгоритм решения этой задачи.

Алгоритм MaxElement (А [0.. n – 1])

// Входные данные: массив вещественных чисел А[0..n – 1]

// Выходные данные: возвращается значение наибольшего

// элемента массива А

begin

maxval <— А[0]

for i <— 1 to n - 1 do

if A[i] > maxval

then maxval <– А[i]

return maxval

end

Очевидно, что в этом алгоритме размер входных данных нужно оценивать по количеству элементов в массиве, т.е. числом n. Операции, выполняемые чаще всего, находятся во внутреннем цикле for алгоритма. Таких операций две: сравнение (А[i] > maxval) и присваивание (maxval <— А[i]). Какую из них считать базовой? Поскольку сравнение выполняется на каждом шаге цикла, а присваивание — нет, логично считать, что основной операцией алгоритма является операция присваивания. (Обратите внимание, что для любого массива размером n количество операций сравнения в рассматриваемом алгоритме постоянно. Поэтому не имеет смысла отдельно рассматривать эффективность алгоритма для худшего, типичного и лучшего случаев.)

Обозначим через f(n) количество выполняемых в алгоритме операций сравнения и попытаемся вывести формулу, выражающую их зависимость от размера входных данных n. Известно, что за один цикл в алгоритме выполняется одна операция сравнения. Этот процесс повторяется для каждого значения счетчика цикла i, которое изменяется от 1 до n – 1 включительно. Поэтому для f(n) получаем следующую сумму:

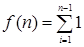
Значение этой суммы очень легко вычислить, поскольку в ней единица суммируется сама с собой n – 1 раз. Поэтому

.

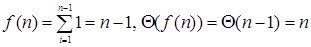Пример 2. Рассмотрим задачу проверки единственности элементов, то есть необходимо попарно сравнить элементы и убедиться, что все элементы массива различны.

АЛГОРИТМ UniqueElements (A [0.. n – 1])

// Входные данные: массив вещественных чисел А[0.. n–1]

// Выходные данные: возвращается значение "true", если все

// элементы массива А различны, и "false"– в противном случае

begin

for i <– 0 to n – 2 do

for j <– i + 1 to n – 1 do if A[i] = A[j]

then return false // и досрочное завершение цикла

return true

end

В этом алгоритме, как и в примере 1, размер входных данных вполне естественно оценивать по количеству элементов в массиве, т.е. числом n. Поскольку в наиболее глубоко вложенном внутреннем цикле алгоритма выполнятся только одна операция сравнения двух элементов, ее и будем считать основной операцией этого алгоритма. Обратите внимание, что количество операций сравнения будет зависеть не только от общего числа n элементов в массиве, но и от того, есть ли в массиве одинаковые элементы, и если есть, то на каких позициях они расположены. Ограничимся рассмотрением наихудшего случая.

По определению наихудший случай входных данных соответствует таком) массиву элементов, при обработке которого количество операций сравнений f(n) будет максимальным среди всей совокупности входных массивов раз­мером n. После анализа внутреннего цикла алгоритма приходим к выводу, что наихудший случай входных данных (т.е. когда цикл выполняется от начала до конца, а не завершается досрочно) может возникнуть при обработке массивов двух типов:

а) в которых нет одинаковых элементов;

б) в которых два одинаковых элемента находятся рядом и расположены в самом конце массива.

В подобных случаях при каждом повторе внутреннего цикла в нашем алгоритме выполняется одна операция сравнения. При этом переменная цикла j последовательно прини­мает значения от i + 1 до n – 1. Внутренний цикл каждый раз повторяется заново при каждом выполнении внешнего цикла. При этом переменная внешнего цикла i последовательно принимает значения от 0 до n – 2. Таким образом, получаем:

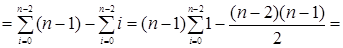
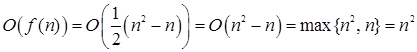
Обратите внимание, что этот результат можно было легко предсказать: в рас­сматриваемом алгоритме в самом худшем случае для массива, состоящего из n элементов, нужно сравнить между собой все (n–1)n /2 различных пар элементов.

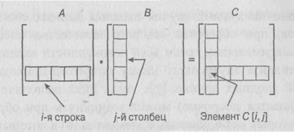
Пример 3. Для двух заданных матриц А и В размером n х n определите временную эффективность алгоритма их умножения С = АВ, основанного на опре­делении этой операции. По определению С – это матрица размером n х n, эле­менты которой являются скалярными произведениями соответствующих строки матрицы А ни столбца матрицы В, как показано ниже.

АЛГОРИТМ MatrixMultiplication (A [0..n – 1, 0.. n – 1],

В [0.. n – 1, 0.. n – 1])

// Выполняется умножение двух квадратных матриц

// размером n х n. Используется алгоритм,

// основанный на определении этой операции

// Входные данные: две квадратные n х n матрицы А к В

// Выходные данные: матрица С = АВ

BEGIN

FOR i 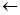0 TO n-1 DO

FOR j 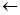0 TO n-1 DO

C[i,j] 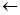0.0

FOR k 0 TO n-1 DO

C[i,j] C[i,j]+A[i, k]*B[k,j]

RETURN C

END

В этом алгоритме размер входных данных соответствует размеру матрицы n. Во внутреннем цикле алгоритма выполняются две арифметические операции: умножение и сложение. В принципе, в качестве основной операции алгоритма можно выбрать как одну, так и другую операцию. Мы рассмотрим случай, когда в качестве основной выбрана операция умножения. Заметьте, что для рассматриваемого алгоритма не обязательно отдавать предпочтение одной из этих операций, поскольку на каждом шаге внутреннего цикла каждая из них выполняется только один раз. Поэтому, подсчитав, сколько раз выполняется одна из операций, мы автоматически подсчитываем и количество выполнения другой операции. А теперь давайте составим сумму для общего числа операций умножения f(n), выполняемых в алгоритме. Поскольку это число зависит только от размера исходных матриц, не требуется отдельно рассматривать наихудший, типичный и наилучший случаи.

Вполне очевидно, что на каждом шаге внутреннего цикла алгоритма выпол­няется только одна операция умножения. При этом значение переменной цикла k последовательно изменяется от нижней границы 0 до верхней границы n – 1. Поэтому количество операций умножения, выполняемых для каждой пары значений переменных i и j, можно записать следующей тройной суммой:

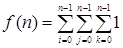
Для вычисления значения этой суммы воспользуемся формулами из следующего раздела:

.

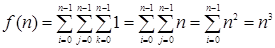Рассматриваемый алгоритм достаточно прост.

Время выполнения алгоритма на конкретном компьютере можно оценить с помощью следующего произведения:

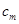— время выполнения одной команды умножения на рассматриваемом компьютере. Чтобы получить более точную оценку, необходимо также учесть время выполнения команд сложения:

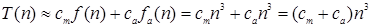
где с_а ~ время выполнения одной команды сложения. Обратите внимание, что полученная оценка отличается от прежней только постоянным множителем, а не порядком роста.