Схемы деления и извлечения квадратного корня
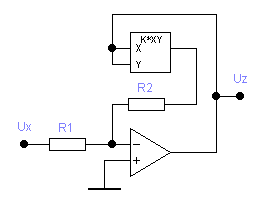
Принцип действия основан на обращении функциональных свойств элемента, включённого в обратную связь ОУ. Если так включить перемножитель, можно получить деление сигналов (а) либо извлечение квадратного корня (б)
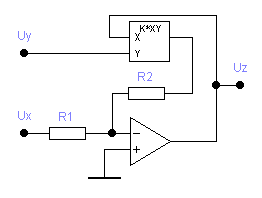
Чтобы доказать справедливость утверждения, применим формальный приём, предположив наличие сопротивления R0 в цепи обратной связи ОУ, тогда выход схемы равен сумме
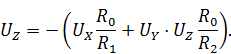
Вынесем R0 за скобки, поделим обе части уравнения на R0, и поменяем знаки
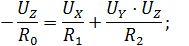
Поскольку 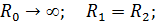 левая часть обращается в ноль, а, разрешив оставшуюся часть относительно UZ, получим
левая часть обращается в ноль, а, разрешив оставшуюся часть относительно UZ, получим
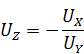
Путём аналогичных рассуждений получим схему извлечения квадратного корня
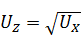
Динамические преобразования сигналов.
Интегрирование
| R |
| C |
| A1 |
| UВХ |
| UВЫХ |
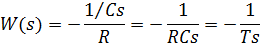
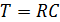
С учётом конечных полосы пропускания 1/T0, усиления k и входного сопротивления 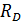
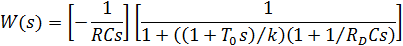
1) Высокочастотная модель описывает поведение на коротких интервалах времени, в частности, на начальном участке процесса интегрирования
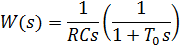
:
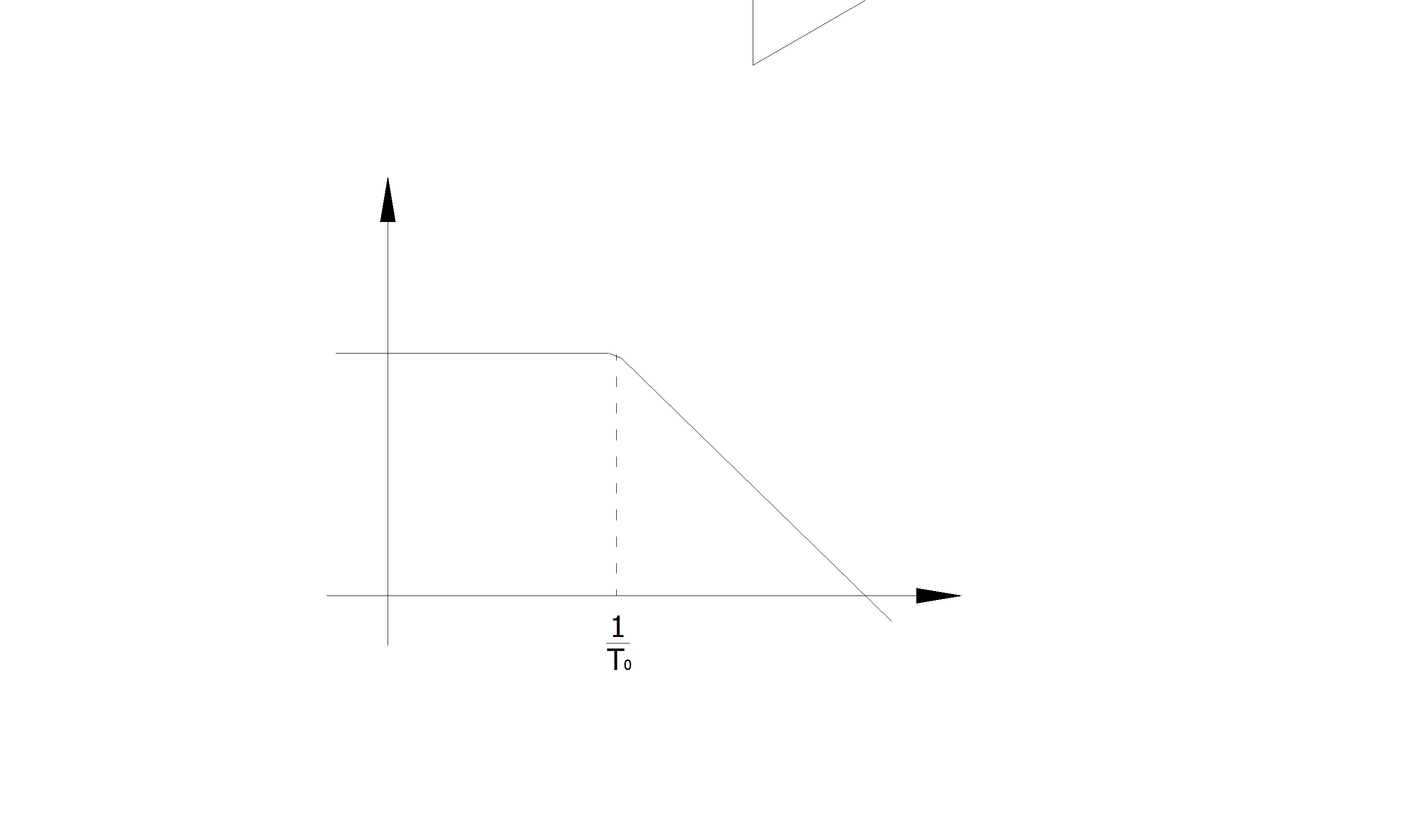 Рисунок 6.1 Частотная характеристика ОУ без ОС Рисунок 6.1 Частотная характеристика ОУ без ОС
| 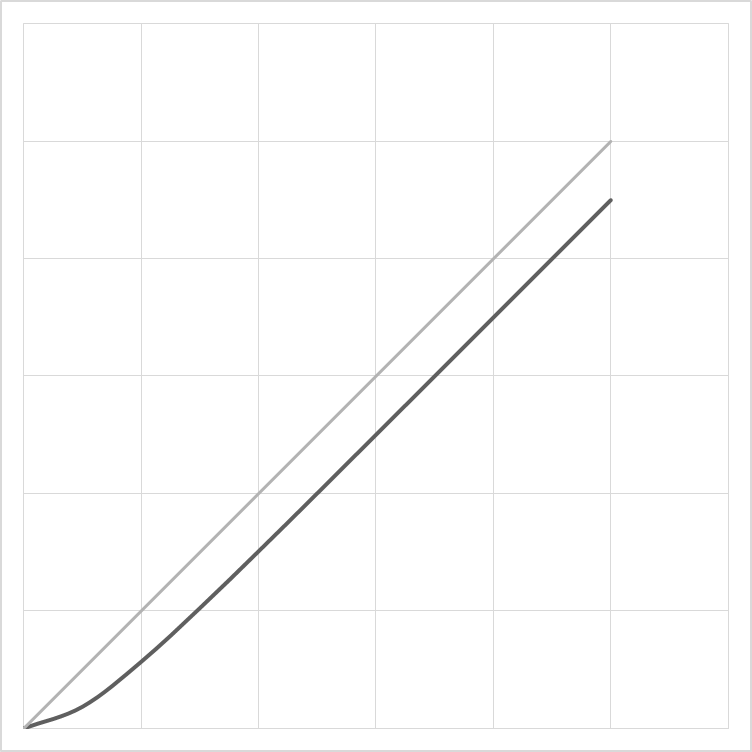
Рисунок 6.2 Начальный участок |
2) Низкочастотная модель (поведение на продолжительных отрезках):
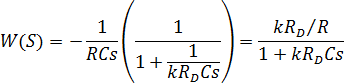
Практическая схема интегратора на ОУ
| Ключ Режим | S1 | S2 | S3 |
| 1k? |
| S1 |
| UIN |
| r1 |
| S3 |
| UREF |
| + |
| - |
| r0 |
| S2 |
| R |
| C |
| A1 |
Режимы:
| 1 - интегрирование входного сигнала | 2 - останов интегрирования |
| 3 - задание начальных условий | 4 - сброс результата |
Для задания начальных условий конденсатор необходимо зарядить до требуемого напряжения. Это осуществляется дополнительной цепью обратной связи 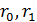 , с передаточной функцией:
, с передаточной функцией:
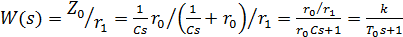 ,
,
представляющей собой ПФ апериодического звена.
Переходной процесс в цепи задания н. у. протекает относительно быстро благодаря тому, что r <<R.
Дифференцирование
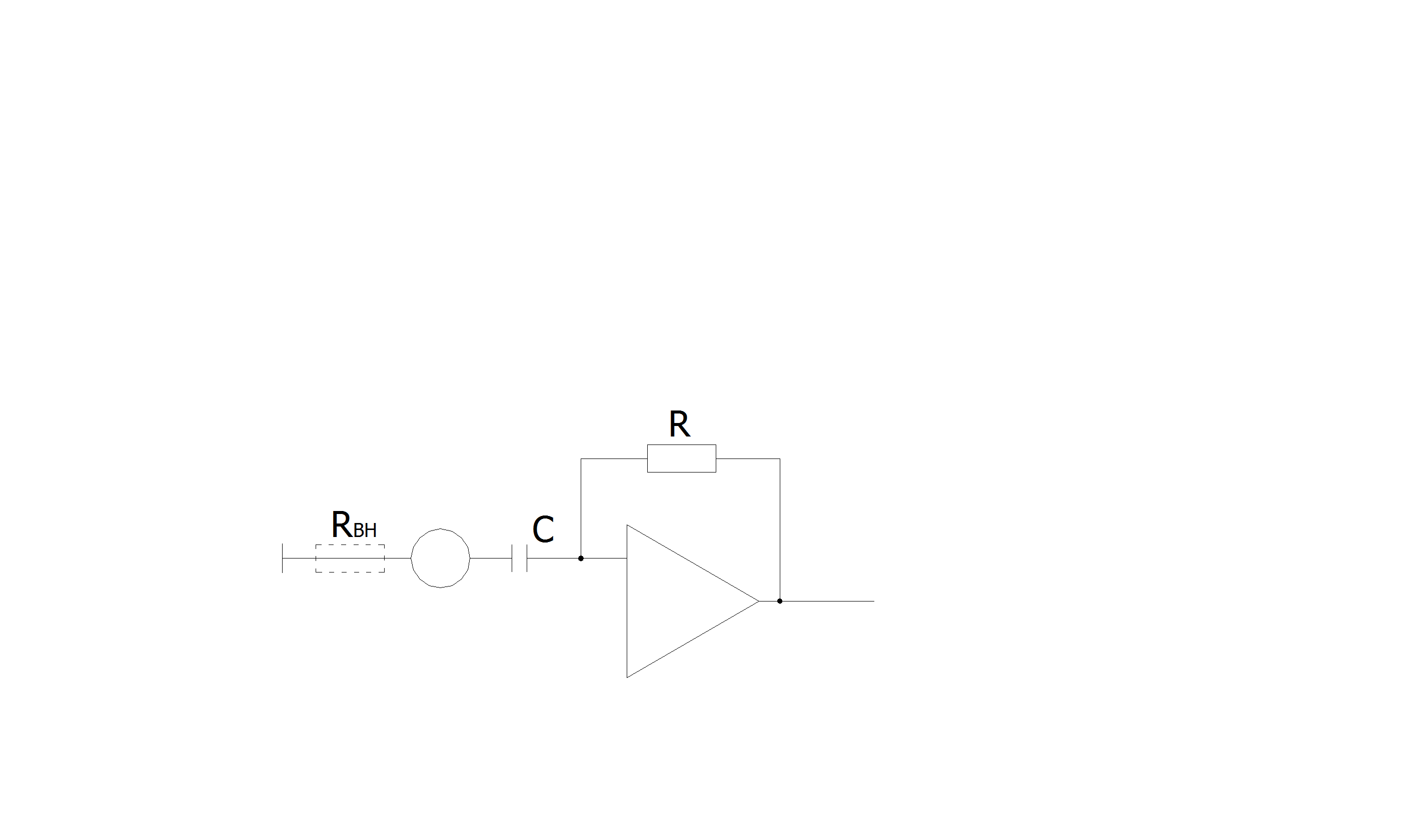
Для идеального источника сигнала
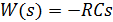
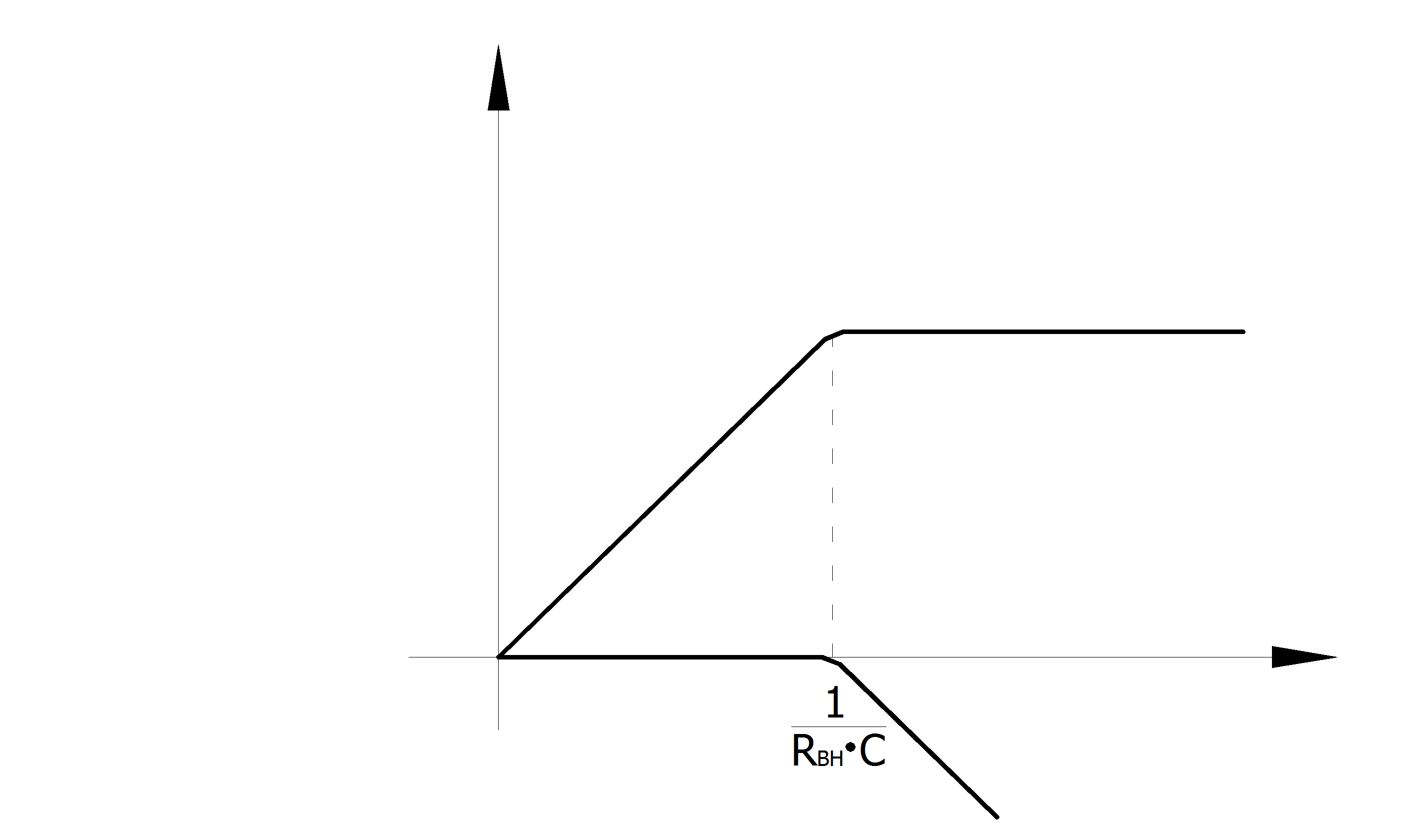
Поскольку источник сигнала обладает внутренним сопротивлением, то
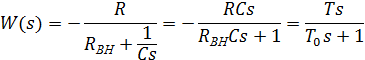
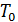 будет сказываться при частотах
будет сказываться при частотах 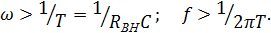
Дата добавления: 2022-02-05; просмотров: 635;











