Использование метода понижения порядка производной для составления схемы моделирования.

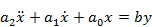
Разрешим относительно старших производных:

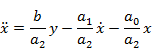
Формируем левую часть уравнения, начиная с суммирующего блока.

Переменные 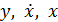считаем условно известными 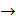получаем 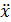(со знаком «минус», поскольку каждый этап преобразования осуществляется инвертирующим ОУ)

Формируем правую часть путём непосредственного интегрирования – получаем последовательно .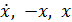

Замыкаем выходы блоков на соответствующие входы с учётом знака, в случае необходимости вводим инверторы.

∑

y

–x

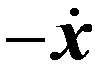
b/a2

a0/a2

a1/a2

∫

∫

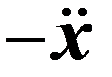
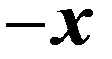
Поскольку в линейной системе действует принцип суперпозиции, операции суммирования и интегрирования можно совместить, в результате схема упрощается

y

–x

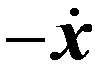
b/a2

a0/a2

a1/a2

∫

∫

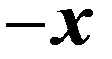
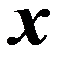
Схема готова – можно переходить к расчёту.

Выбор масштабных коэффициентов:

На основе 3-й системы электромеханических аналогий все переменные исходных уравнений представлены напряжениями в различных точках модели.

Масштабный коэффициент показывает, какое напряжение соответствует единице физической переменной: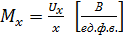

Для повышения точности решения задачи стремятся использовать всю шкалу возможных значений машинных переменных, поэтому масштаб стремятся выбирать из условия: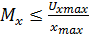

Правильным выбором масштабных коэффициентов можно уменьшить разброс величин коэффициентов машинных уравнений, а, следовательно, повысить точность решения. Необходимо лишь не допускать выхода машинных переменных за границы допустимых значений.

ПРИМЕР:

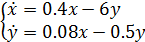начальные условия:

Введём масштабные коэффициенты:

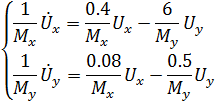
Разрешим относительно старших производных:

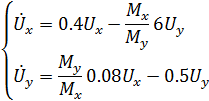
Для уменьшения разброса коэффициентов примем

.

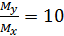Тогда: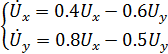

При этом если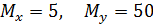

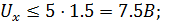
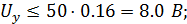
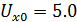
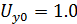
2.5.2. Выбор масштаба времени:

Обусловлен желаемым временем решения задачи с учётом ограничений, накладываемых частотными характеристиками решающих блоков, регистрирующих устройств, коммутирующих элементов, а также погрешностями интегрирующих блоков, обусловленных, например, утечками в конденсаторах и т. д.

Масштаб времени входит в машинные уравнения в виде множителей при производных, зависящих от порядка производных:

; ; .

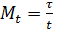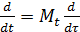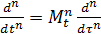Стремление ускорить масштаб времени обусловливается как желанием быстрее получить результат, так и уменьшить погрешность от дрейфа. Однако ускорение ограничено возрастанием величин производных, что приводит к насыщению решающих блоков (нелинейный режим - ошибка)

Правильный выбор 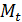может способствовать сокращению разброса параметров параметров при реализации жёстких уравнений.

ПРИМЕР:

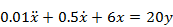
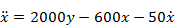
Перейдём к машинному уравнению:

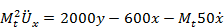
Разрешаем относительно старшей производной

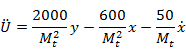
Пусть

;

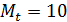тогда

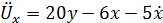
Замена переменных:

Для решения уравнений, в которых независимая переменная не являются временем, осуществляют замену этой переменной на время путём подстановки. ( )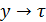

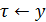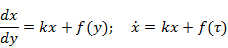
и далее решают обычным способом как обычное дифференциальное уравнение временным аргументом.

2.5.3. Расчёт коэффициентов передачи решающих блоков:

После составления функциональных схем набора требуется определить коэффициенты передачи по входам решающих блоков. Порядок может быть следующий:

По функциональной схеме записать уравнения, связывающие машинные переменные входах и выходах решающих блоков.

Полученную систему уравнений разрешить относительно входных и выходных переменных моделируемой системы.

Машинные переменные заменить исходными с учётом масштабных коэффициентов.

Приравнивая коэффициенты при соответствующих производных исходных и полученных уравнений, получают систему уравнений, связывающую коэффициенты исходных уравнений с коэффициентами передачи решающих блоков.

ПРИМЕР:

Колебательное звено: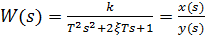

Уравнение в операторном виде:

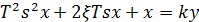
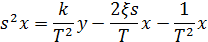
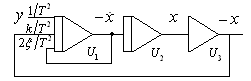
Для функциональной схемы:

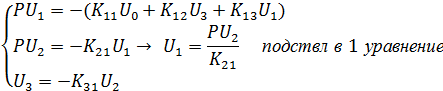
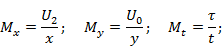
Подставляем: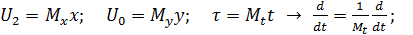

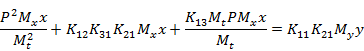
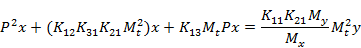
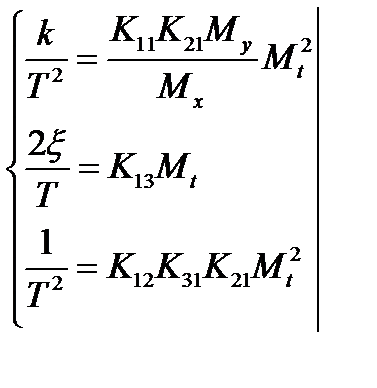
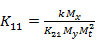
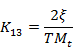
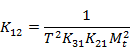
Поскольку число уравнений меньше числа неизвестных коэффициентов, некоторые из них можно задавать из условия распределения коэффициентов по блокам в пределах максимально допустимых значений.

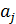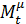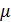Общее правило: коэффициент исходного уравнения равен произведению коэффициента передачи контура, внутри которого определяется переменная, стоящая при определяемом коэффициенте, умноженному на , где - число интеграторов в контуре.

Коэффициент в правой части исходного уравнения равен произведению К передачи от места приложения воздействия до выхода системы, умноженному на отношение 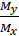входных и выходных переменных и 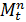, где n – порядок дифференциального уравнения.

Начальные условия преобразуем в соответствием с масштабным соотношением, т.е. ; ; .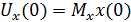

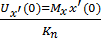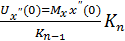При программировании систем ДУ функциональные схемы строят отдельно для каждого уравнения и затем осуществляют необходимые связи.

ПРИМЕР: Моделирование движения ЛА в вертикальной плоскости.

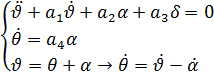
Здесь

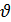- тангаж

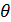- траекторный угол

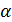- угол атаки

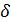- угол поворота руля высоты

Коэффициенты отражают свойства ЛА

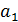- аэродинамическое демпфирование

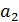- статическая устойчивость

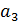- эффективность руля высоты

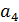- маневренные возможности ЛА

Приведём к виду удобному для набора:

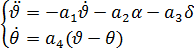
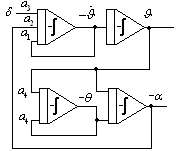
2.5.4. Воспроизведение дробно-рациональных передаточных функций
методом комбинирования производных

Преобразуем исходную ПФ

,

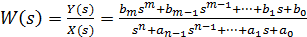вводя новую переменную u:

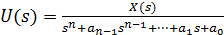. (1)

В результате получаем

,

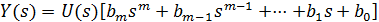в дифференциальной форме:

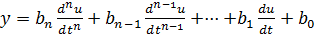. (2)

Выражение (1) также можно записать в дифференциальной форме:

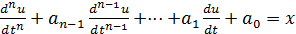. (3)

Для составления структурной схемы набора необходимо сначала «набрать» уравнение (3) по методу понижения порядка производной, а затем образовать искомую переменную у в виде суммы производных от и с соответствующими коэффициентами. Значения производных 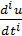получаются непосредственно с соответствующих выходов интеграторов при решении уравнения (3). Некоторое упрощение схемы набора может получиться, если в уравнении (2) исключить старшую производную u подстановкой её значения из уравнения (3).

В результате приходим к уравнениям

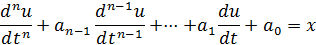
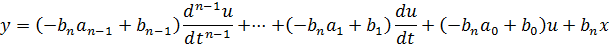
Функциональная схема реализации этих уравнений для т = п = 3приведена на рисунке. В общем случае для набора необходимо иметь п + 3 решающих блока. Для определения коэффициентов при наборе задачи не требуется выполнения трудоёмких вычислений.

∫

∫

∫

∫

∑

x

–x

b3

b3a2+b2

–b3a0+b0

–b3a1+b1

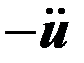
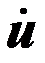
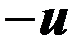
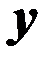
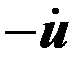
Функциональная схема реализации дифференциального уравнения,
составленная по методу комбинирования производных.