Сети Петри. Основные сведения

Широко распространенным способом представления параллельных вычислительных процессов являются сети Петри (Petri). Они были разработаны в 1962 г. и предназначались, главным образом, для координации асинхронных потоков команд в операционных системах, компиляторах, коммуникационных протоколах и алгоритмах обновления информации в распределенных базах данных.

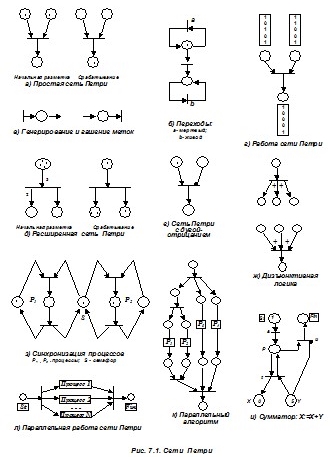
Сеть Петри представляет собой ориентированный граф, имеющий в своем составе (рис. 4.1):
а) множество узлов (позиций, условий, мест, вершин) (place);
б) множество переходов (событий) (transition);
в) множество направленных дуг (ребер), соединяющих узлы с переходами.

Узлы могут быть свободными или содержать метки (признаки, маркеры, фишки) (token), которые определяют условия выполнения соответствующей вычислительной операции.

Узлы (позиции) обозначаются кружками, переходы – чертой, а метки– точками внутри узла.

Простые сети Петри. На рис. 4.1а показана простая сеть Петри, которая имеет один переход, три ребра и три узла, два из которых помечены (маркированы).

Каждый переход имеет, как правило, свои входные (стартовые) и выходные узлы. На рис. 4.1а (слева) входными являютсядва помеченных узла, а выходным – непомеченный узел.

Переход называется активизированным (живым), если все его входные узлы помечены. Переход называется мертвым, если он не активизирован.

Например, переход на рис. 4.1а является активизированным (живым), поскольку ребраиз обеих узлов, входящих в переход, являются помеченными.

Переход ана рис. 4.1б является мертвым, поскольку метка может "провалиться" в нижний цикл и переход а уже никогда не сработает. В то же время переход b является живым.

Переход, не имеющий ни одного входного ребра, всегда активизирован и может постоянно генерировать новые метки и подавать их на свои выходные узлы (рис. 4.1в).

Переход, имеющий только одно входное ребро и не имеющий ни одного выходного ребра, всегда активизирован (если он помечен) и может постоянно поглощать (гасить) метки (рис. 4.1в).

Переход может срабатывать, если все его входные узлы содержат хотя бы одну метку (рис. 4.1а). При этом число меток во всех входных узлах данного перехода уменьшаются на единицу и помечаются все выходные узлы этого перехода. Если в выходном узле уже была метка, то она сохраняется.

Срабатывание перехода соответствует реализации некоторой вычислительной операции. Последовательность срабатываний переходов называется исполнительной последовательностью сети Петри. Ее можно представить в виде бинарных цифр двоичного ряда, отображающих движение меток при срабатывании переходов (рис. 4.1г).

Сеть Петри называется живой, если в каждом очередном состоянии исполнительной последовательности активизирован хотя бы один из ее переходов. Сеть Петри называется мертвой (тупиковой, заблокированной), если в ней нет активизированных переходов.

Расширенные сети Петри. Сети Петри становятся существенно эффективнее при введении в них некоторых расширений, к числу которых относятся следующие:
а) каждый узел сети может иметь любое число меток (рис.4.1.д), которое допускается указывать числом;

б) на каждой дуге может указываться ее вес, т.е. число меток, которые необходимо удалить из соответствующего входного узла (и добавить в выходные узлы) для срабатывания перехода (рис. 4.1д); если вес дуги не указан, то он считается равным единице;

в) среди дуг сети могут быть так называемые дуги-отрицания, которые изображаются кружком на конце вместо стрелки и не имеют веса (рис. 4.1е); они всегда направлены от узла к переходу и не могут иметь обратного направления;

г) в сети Петри можно расширить правило срабатывания путем введения дизъюнктивной логики "или" (рис. 4.1ж) (обозначены знаком "+"): при срабатывании перехода (на верхнем рисунке) только один из выходных узлов получает метку; переход срабатывает (на нижнем рисунке), если хотя бы один из входных узлов имеет метку.

Ввод в рассмотрение дуг-отрицаний (рис.4.1е) обуславливает использование обновленных правил активизации и срабатывания переходов. К числу таких правил относятся следующие:
- переход с двумя входными узлами активизируется, если число меток в узле с обычной дугой больше или равно весу дуги, а узел с дугой-отрицанием не имеет меток;
- при срабатывании перехода число меток во входных узлах с обычными дугами уменьшается в соответствии с весами дуг, а в узлах с дугами-отрицаниями число меток остается неизменным.