Примеры построения графов параллельных алгоритмов. Графы вычислительных процессов в ПВМ

Пример. Построим граф алгоритма, представленного в табл.2.1 (рис.3.1). Его вершинами являются операции, осуществляемые на соответствующих ярусах (шагах алгоритма). Входными его вершинами являются исходные данные а_i (i =1…8), а дугами – информационные связи между операциями (вершинами).

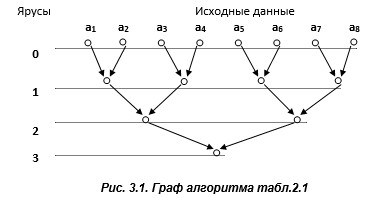
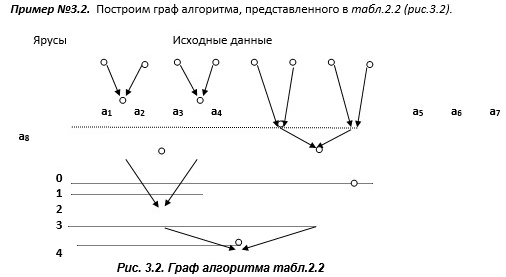
Как видно из рисунков 3.1 и 3.2, графы алгоритмов ПФ №1 и ПФ №2 совпадают, поскольку они задают эквивалентные формы алгоритмов. Эти графы являются изоморфными, поскольку их вершины и дуги сохраняют смежность и ориентацию (см. раздел.3.1).

Пример № 3.3. Для выявления параллельности алгоритма часто используют решетчатыеграфы. Процесс построения такого графа сводится к выбору для данного алгоритма прямоугольной системы координат, связанной с индексами переменных. В этой системе строится регулярная прямоугольная решетка с вершинами графа в ее узлах в соответствии с индексами переменных, определяющих выполняемые операции.

Пусть требуется построить решетчатый граф алгоритма вычисления произведения двух квадратных матриц размерности n х n: Х = А × В.

Алгоритм вычислений представим в вде следующего соотношения: x_ijk = x_ijk-1 + a_ik b_jk , ( i , j , k =1…n ).Определим базовую операцию в виде: x + ab.

В узел с фиксированными координатами ( i , j , k) поместим вершину, соответствующую операции x_ijk-1 + a_ik b_jk. (рис. 3.3).Поскольку a_ik и b_jk задают входные данные алгоритма, то в вершину с координатами ( i , j , k) будет направлена только одно ребро, выходящее из вершины с координатами ( i , j , k-1 ).Это означает, что при числе процессоров, равном n², можно осуществить параллельное вычисление n² координат (т. е. координат одного уровня) за один шаг и решить задачу за n-1шагов. Это стало возможным благодаря удачному выбору базовой операции и системы координат.

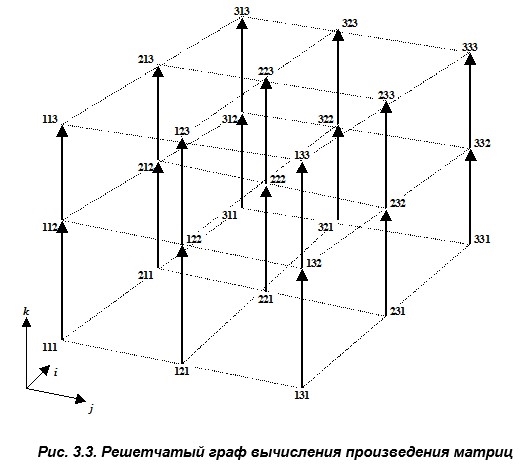
Если вершины решетчатого графа принадлежат замкнутому параллелепипеду размерности n с ребрами длиной l_i, ( i=1…n ), то высота параллельного алгоритма определяется соотношением: h £ S l_i, +1 ( i=1…n ).

Графы вычислительных процессов в ПВМ. Вычислительный процесс в ПВМ можно представить в виде ориентированного графа, вершинами которого являются операции (операторы), а дугами – каналы передачи информации между вершинами. Существует три основных способа представления графов параллельной обработки данных в ПВМ.

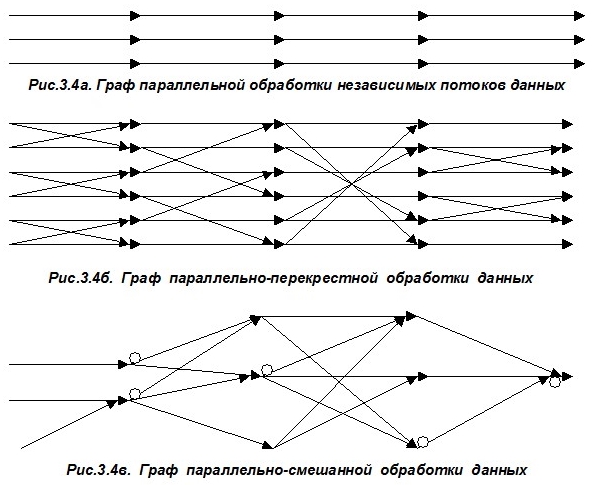
1) Граф параллельной обработки независимых потоков данных (рис.3.4а) характеризуется наличием нескольких идентичных независимых параллельных ветвей с одинаковым числом операций (вершин) в каждой ветви. Такими графами описывается, например, процесс обработки потоков данных, поступающих с однотипных датчиков информации.

2) Граф параллельно-перекрестной обработки данных (рис.3.4б) отличается наличием перекрестных регулярных связей между операторами параллельных ветвей. Такими графами описываются широкие классы задач матричной алгебры, линейного программирования, спектральной обработки сигналов, прямое и обратное преобразования Фурье, Адамара и других задач, которые хорошо поддаются распараллеливанию.

3) Граф параллельно-смешанной обработки данных (рис.3.4в) представляет собой комбинацию из первых двух видов графов и содержит в дополнение к ним ветви вычислений с произвольным набором операторов и связей. В каждый момент времени в таком графе имеются множества вершин операторов, готовых к работе (отмечены кружками). Ветви включаются в работу в зависимости от условий, вырабатываемых в различных частях графа.