Неперервний випадок

Якщо різних значень у вибірці буде багато, або всі вони будуть різними, то складена таблиця частот не демонструє особливостей вибірки. У цьому випадку поступають таким чином:

Перший етап. Увесь проміжок зміни значень вибірки від найменшого до найбільшого розбивають на інтервали або на класи. Важливе значення має вибір оптимальної величини інтервалу і правильне включення варіант у відповідний інтервал. Для цього в кожному інтервалі слід розрізняти верхню і нижню межу. Розмах всієї вибірки дорівнює 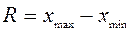. Оптимальна кількість інтервалів (т) як правило лежить у межах від 5 до 15. Нижню межу і‑го інтервалу позначають х_і(min), верхню – х_і(mаn), де і змінюється від 1 до т.

Величина інтервалу h_i є різниця між максимальним та мінімальним значенням ознаки в кожному класі h_i= х_і(mаn)- х_і(min)

Інтервали зазвичай беруть однакової довжини. Вона повинна бути такою, щоб ряд не був громіздкий і щоб у ньому не зникали особливості ознаки, що досліджується. Ширину рівних інтервалів визначають за формулою Стерджеса

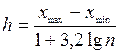де n – об’єм вибірки

або

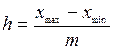, де т – кількість класів.

Другий етап. Розбивши ряд на інтервали підраховують число значень із вибірки (частоти), які потрапили в кожний інтервал, а потім відносні частоти. В результаті одержуємо інтервальну таблицю частот.

				...
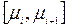
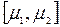
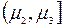
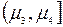
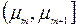
ki	k1	k2	k3	...	km
ni=	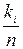n1=	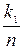n2=	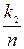n3=	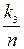...	nm=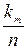

де n – об’єм вибірки,

т – число інтервалів,

k_i–кількість значень, що потрапила в і-тий інтервал (частота),

n_i= 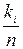– відносна частота попадання в і-тий інтервал,

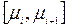– інтервал,

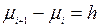– ширина інтервалу

Третій етап. Графічною ілюстрацією таблиці частоти є гістограма та полігон.

Означення. Гістограмою частот (відносних частот) називають ступінчасту фігуру, що складається з прямокутників основами яких є довжини інтервалів значень вибірки, а висоти дорівнюють .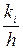

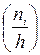Площа і-го стовпчика дорівнює п_і , а площа усієї гістограми відносних частот дорівнює одиниці.

Полігон для інтервальної таблиці частоти легко дістати з гістограми. Для цього досить сполучити відрізками середини верхньої сторони прямокутників.

Приклад 2. 25 випускників школи писали тест з математики. Кожен учень отримав певну кількість балів: 75,145,150,180,125, 150,150,165,95,135,130,70,130,105,135,135,100,160,60,85,120,60,145,150,135

Потрібно побудувати інтервальну таблицю частот та графічно зобразити її у вигляді гістограми та полігону.

Визначаємо х_min=60, х_mах=180. Всі значення вибірки знаходяться на відрізку 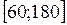, отже R=180-60=120. Розіб’ємо розмах варіації, наприклад, на 6 класів, маємо 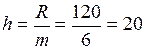. Якщо використати формулу 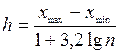, то отримаємо, що h»22.

Будуємо інтервальну таблицю частоти

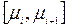
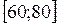
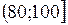
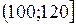
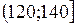
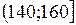
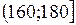
ki
ni=	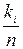0,16	0,12	0,08	0,28	0,28	0,08

Відповідна гістограма та полігон частот матиме вигляд