Числові характеристики основних розподілів
| Числові характеристики Розподіли | М(Х) | D(X) | 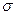 (X) (X)
| |
| Розподіли дискретної випадкової величини | Біноміальний | |||
| Пуассона | ||||
| Геометричний | ||||
| Розподіли неперервної випадкової величини | Рівномірний | |||
| Показниковий | ||||
| Нормальний |
ІІ. Модульний тестовий контроль передбачає перевірку теоретичних знань студентами основних понять, формул, формулювання теорем, правил та умов їх застосування при розв’язуванні практичних завдань. Тест є комплексом завдань трьох рівнів (А-низький, Б-достатній, В –високий). Максимальна кількість балів за тест –11( за 1 запитання рівня А – 0,2б., за 1 запитання рівня Б – 0,5б., за 1 запитання рівня В –1б.)
Орієнтовні запитання тесту
Рівень А
1. Випадковою називають величину, яка
1) в результаті випробування приймає одне і тільки одне можливе дійсне значення, наперед невідоме і залежне від випадкових обставин.
2) при умовах що розглядаються може здійснитися, а може й не здійснитися.
3) в результаті випробування приймає скінчену або нескінчену кількість значень, наперед невідомих
2. Випадкова величина Х називається дискретною,
1) яка може приймати відокремлені ізольовані одне від одного числові значення з відповідними ймовірностями..
2) якщо її функцію розподілу можна подати у вигляді
F(x)= 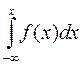 , де
, де 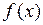 – диференціальна функція розподілу.
– диференціальна функція розподілу.
3) яка може приймати будь-яке числове значення з деякого скінченого або нескінченного інтервалу (а;в).
3. Співвідношення, що встановлює зв’язок між можливими значеннями випадкової величини та їх ймовірностями називається...(вкажіть невірну відповідь)
1) законом розподілу випадкової величини;
2) щільністю випадкової величини;
3) числовою характеристикою випадкової величини.
4. Чи справедлива нерівність 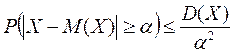
1) так;
2) ні.
5. Числовою характеристикою випадкових величин не є:
1) математичне сподівання;
2) середнє квадратичне відхилення;
3) закон розподілу.
6. Чи справедлива нерівність 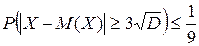
1. так;
2. ні.
7. Імовірність того, що випадкова величина Х прийме значення менше х, називають:
1) інтегральною функцією розподілу;
2) диференційованою функцією розподілу;
3) неперервною функцією розподілу.
8. Диференційованою функцією розподілу неперервної випадкової величини називають:
1) первісну від її інтегральної функції розподілу;
2) похідну від її інтегральної функції розподілу;
3) похідну першого порядку від її інтегральної функції розподілу.
9. Дисперсію дискретної випадкової величини Х доцільно знаходити за формулою…
1) D(Х)=M((Х-M(Х))2);
2) D(Х)=M(Х2)-(M(Х))2;
3) D(Х)=(σ(Х))2.
10. Математичне сподівання дискретної випадкової величини обчислюють за формулою:
1) М(Х)= 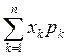 ;
;
2) М(Х)= 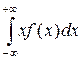 ;
;
3) D(X)=M(X2)-(M(X))2.
Рівень Б
1. На малюнку зображено графік
 |
1) нормального закону розподілу;
2) показникового закону розподілу;
3) рівномірного закону розподілу.
2. Випадкову величину Х називають розподіленою нормально, якщо щільність її ймовірностей має вигляд
1) 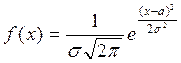 ;
;
2) 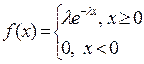 ;
;
3) 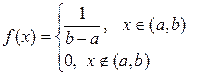 .
.
3. Оберіть неправильне твердження:
1) Математичне сподівання сталої величини є сама ця стала М(С)=С.
2) Сталий множник можна виносити за знак математичного сподівання М(СХ)=СМ(Х).
3) Математичне сподівання суми двох випадкових величин дорівнює добутку їх математичних сподівань.
4. Оберіть правильне твердження:
1) D(C)=0, C – стала величина;
2) сталий множник можна винести за знак дисперсії;
3) дисперсія різниці незалежних випадкових величин дорівнює різниці їх дисперсій.
5. Розподілом дискретної випадкової величини є
1) рівномірний розподіл;
2) показниковий;
3) біноміальний.
6. Математичне сподівання НВВ, розподіленої за біноміальним законом розподілу, знаходять за формулою:
1) np;
2) npq
3) 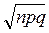
7.Для будь-якої випадкової величини Х ймовірність того, що вона відхиляється від свого математичного сподівання більше, ніж на число 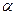 , завжди менша, ніж
, завжди менша, ніж
1) 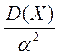 ;
;
2) 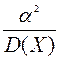 ;
;
3) 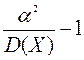 .
.
8. Ймовірність настання принаймні однієї з подій А1, А2, ..., Ап , незалежних в сукупності, знаходиться за формулою:
1) 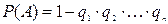 ;
;
2) 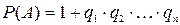 ;
;
3) 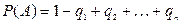 .
.
9. Чи справедлива рівність 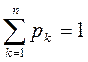 , де рк– ймовірність значень ДВВ,
, де рк– ймовірність значень ДВВ,
1) так;
2) ні.
10. Аналітичний вираз 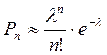 , де
, де 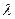 >0, п=0,1,2,...має назву
>0, п=0,1,2,...має назву
1) формула Пуассона;
2) локальна теорема Муавра – Лапласа;
3) інтегральна теорема Муавра – Лапласа.
Рівень В
1. Нехай Х – випадкова величина, яка має біноміальний розподіл з параметрами n та р. Відомо, що М(Х)=12; D(Х)=4. Тоді кількість випробувань дорівнює
1) 18;
2) 24;
3) 9.
2. Дискретна випадкова величина задана законом розподілу
| хі | |||
| рі | 0,3 | 0,5 | 0,2 |
Математичне сподівання дорівнює:
1) 5400;
2) 5450;
3) 6000.
3. Автобус деякого маршруту йде точно за розкладом в інтервалі 6 хвилин. Знайти ймовірність того, що пасажир, котрий підійшов до зупинки, буде чекати наступного автобуса протягом з хвилин. Якою формулою потрібно скористатися для обрахунку ймовірності?
1) 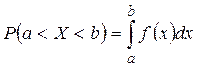 ;
;
2) 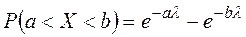
4. Математичне сподівання і середнє квадратичне відхилення нормально розподіленої неперервної випадкової величини Х відповідно рівні 12 і 4. Знайти ймовірність того, що в результаті випробування Х прийме значення з інтервалу (14;16).
Який вираз веде до правильного результату?
1) 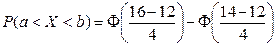 ;
;
2) 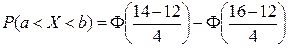 ;
;
3) 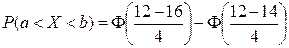 .
.
ІІІ. Модульна контрольна робота передбачає розв’язання двох задач, яке оцінюється 2,5 балами.
Орієнтовні варіанти задач для мкр
Задача 1
1. Двоє друзів при закінченні університету одержали спеціальності інженера і менеджера. Ймовірність того, що при закінченні університету випускник-інженер одразу влаштується на роботу дорівнює 0,7, для випускника-менеджера ця ймовірність складає 0,8. Дискретна випадкова величина – кількість друзів, що влаштувалися на роботу. Знайти закон розподілу ДВВ, числові характеристики та функцію розподілу.
2. Відрізок поділено на дві рівні частини. На цей відрізок кинуто три точки. Попадання точки в будь-яке місце відрізку рівноможливе. Дискретна випадкова величина – кількість точок, що потрапили на першу половину відрізку. Знайти закон розподілу ДВВ, числові характеристики та функцію розподілу.
3. Проводиться вимірювання зросту трьох студентів. Ймовірність того, що студент має зріст вище ніж 1м 85см складає 0,3. Вимірювання припиняється при виявленні студента зі зростом більше ніж 1м 85см. Дискретна випадкова величина – кількість досліджених студентів. Знайти закон розподілу ДВВ, числові характеристики та функцію розподілу.
4. Дискретна випадкова величина Х – кількість разів появи 4 очок при двох підкиданнях одного грального кубика. Знайти закон розподілу ДВВ, числові характеристики та функцію розподілу.
5. Дискретна випадкова величина Х – кількість разів появи 4 очок при підкиданні двох гральних кубиків. Знайти закон розподілу ДВВ, числові характеристики та функцію розподілу.
6. З колоди карт (36 шт.) беруть дві карти. Дискретна випадкова величина Х – кількість дам серед взятих 2-х карт. Знайти закон розподілу ДВВ, числові характеристики та функцію розподілу.
7. На шляху руху автомобіля три світлофори, кожен з яких дозволяє або забороняє рух автомобіля з ймовірністю 0,5. Дискретна випадкова величина Х – кількість світлофорів, які водій проїхав без зупинки.Знайти закон розподілу ДВВ, числові характеристики та функцію розподілу.
8. Проводиться тестування чотирьох людей. Ймовірність того, що обрана людина виявиться екстравертом – 0,4. Дослідження припиняється при першому виявленні екстраверта. Дискретна випадкова величина – кількість досліджених людей. Знайти закон розподілу ДВВ, числові характеристики та функцію розподілу.
9. В ящику знаходяться ялинкові прикраси: 7 червоного кольору, та 3 – жовтого. Навмання беруть 2 прикраси. Дискретна випадкова величина – число червоних прикрас серед відібраних. Знайти закон розподілу ДВВ, числові характеристики та функцію розподілу.
10. В ящику знаходяться пачки морозива: 6 - пломбір, та 4 – кавове. Навмання беруть 2 пачки. Дискретна випадкова величина – число пачок з пломбіром серед відібраних. Знайти закон розподілу ДВВ, числові характеристики та функцію розподілу.
Задача 2
1. Випадкова величина Х задана інтегральною функцією
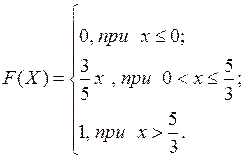
Знайти диференціальну функцію розподілу, числові характеристики, а також ймовірність попадання значення випадкової величини в інтервал (-1;0).
2. Випадкова величина Х задана інтегральною функцією
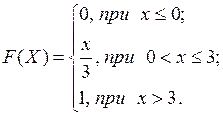
Знайти диференціальну функцію розподілу, числові характеристики, а також ймовірність попадання значення випадкової величини в інтервал (0;1).
3. Випадкова величина Х задана інтегральною функцією розподілу
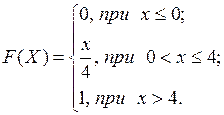
Знайти диференціальну функцію розподілу, числові характеристики, а також ймовірність попадання значення випадкової величини в інтервал (-1;0).
4. Випадкова величина задана функцією розподілу:
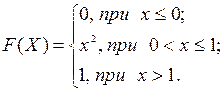
Знайти диференціальну функцію розподілу, числові характеристики, а також ймовірність попадання значення випадкової величини в інтервал (-2; 0,5).
5. Дано інтегральну функцію неперервної випадкової величини Х:
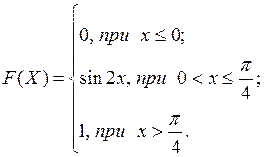
Знайти диференціальну функцію f(x), числові характеристики, а також ймовірність попадання значення випадкової величини в інтервал (0; 0,5).
6. Випадкова величина Х задана інтегральною функцією
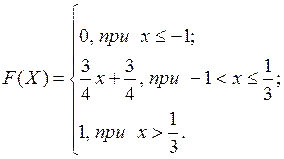
Знайти диференціальну функцію f(x), числові характеристики, а також ймовірність попадання значення випадкової величини в інтервал (0, 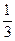 ).
).
7. Випадкова величина Х задана інтегральною функцією розподілу
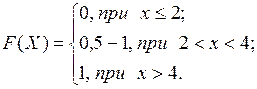
Знайти диференціальну функцію f(x), числові характеристики, а також ймовірність попадання значення випадкової величини в інтервал (2;3).
8. Функція розподілу випадкової величини Х має вигляд
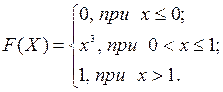
Знайти диференціальну функцію f(x), числові характеристики, а також ймовірність попадання значення випадкової величини в інтервал (0;1).
9. Неперервна випадкова величина Х розподілена за законом, заданим диференціальною функцією
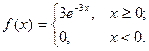
Знайти числові характеристики, а також ймовірність попадання значення випадкової величини в інтервал (0,13;0,7).
10. Неперервна випадкова величина задана інтегральною функцією розподілу: 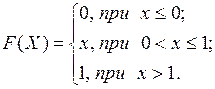
Знайти диференціальну функцію розподілу, числові характеристики, а також ймовірність попадання значення випадкової величини в інтервал (0,5;1).
Дата добавления: 2022-02-05; просмотров: 724;











