Структура общего решения неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа
Пусть дано неоднородное дифференциальное уравнение
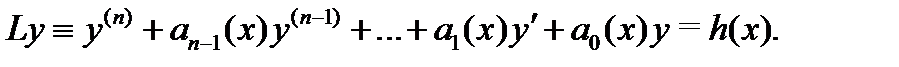
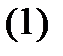
Докажем следующее утверждение.
Теорема 1(о структуре общего решения неоднородного уравнения). Если в уравнении (1) все коэффициенты 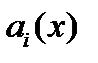 и правая часть
и правая часть 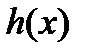 непрерывны на отрезке
непрерывны на отрезке 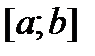 , то общее решение уравнения (1) (на этом отрезке) имеет вид
, то общее решение уравнения (1) (на этом отрезке) имеет вид
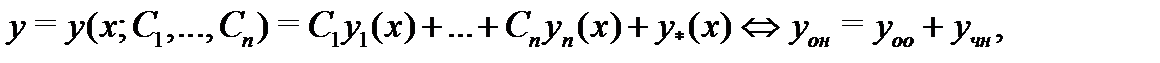
где 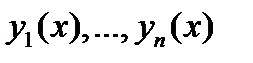 – фундаментальная система решений соответствующего однородного уравнения
– фундаментальная система решений соответствующего однородного уравнения 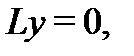 а
а 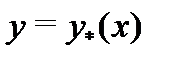 – частное решение неоднородного уравнения (1),
– частное решение неоднородного уравнения (1), 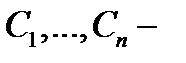 произвольные постоянные.
произвольные постоянные.
Доказательство. Применяя оператор 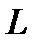 к функции (2), будем иметь
к функции (2), будем иметь
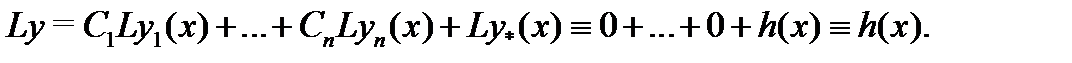
Это означает, что функция (2) является решением уравнения (1) при произвольных значениях постоянных 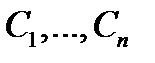 . Пусть теперь
. Пусть теперь 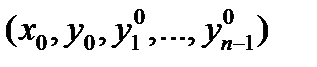 –- произвольная точка в
–- произвольная точка в 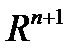 (
( 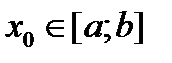 ). Покажем, что решение
). Покажем, что решение 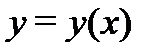 задачи Коши
задачи Коши
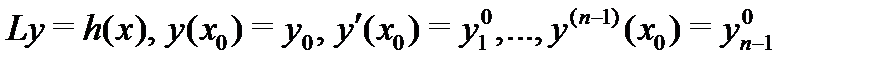
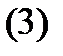
можно получить из (2) выбором определенных значений 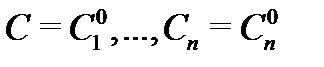 постоянных. Подчиняя (2) условиям (3), будем иметь
постоянных. Подчиняя (2) условиям (3), будем иметь
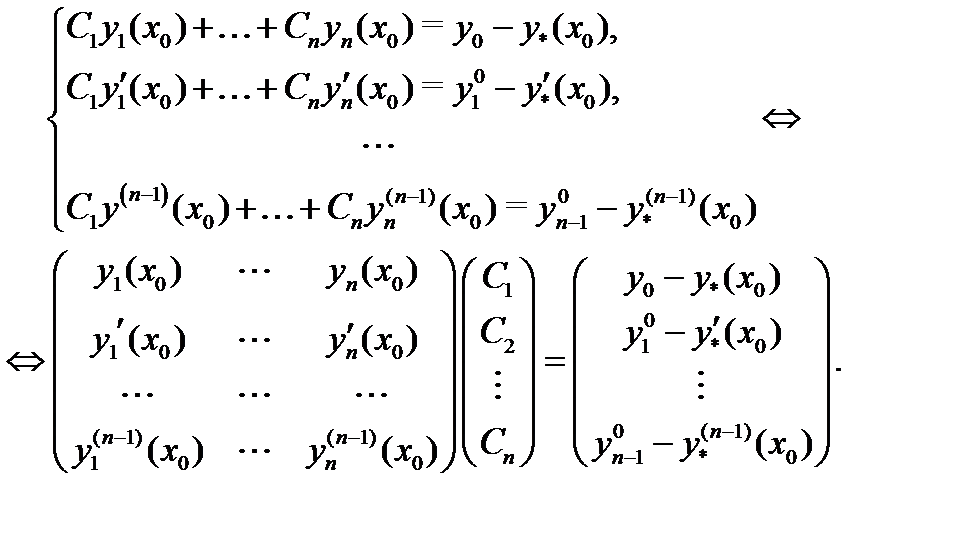
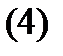
Определитель этой системы совпадает с вронскианом 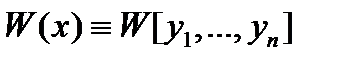 в точке
в точке 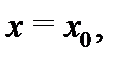 и поскольку фундаментальная система решений
и поскольку фундаментальная система решений 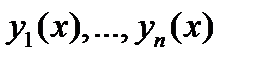 линейно независима на отрезке
линейно независима на отрезке 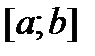 , то указанный определитель системы (4) не равен нулю. Следовательно, система (4) имеет единственное решение
, то указанный определитель системы (4) не равен нулю. Следовательно, система (4) имеет единственное решение 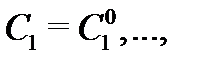
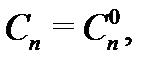 а значит функция
а значит функция 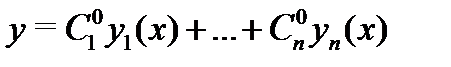 является решением задачи Коши (3). Тем самым показано, что функция (2) является общим решением неоднородного уравнения (1). Теорема доказана.
является решением задачи Коши (3). Тем самым показано, что функция (2) является общим решением неоднородного уравнения (1). Теорема доказана.
2.Метод вариации произвольных постоянных Лагранжа
Согласно теореме 1 поиск общего решения неоднородного дифференциального уравнения (1) сводится к двум процедурам:
1) построение фундаментальной системы решений 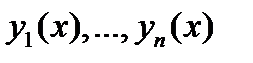 соответствующего однородного уравнения;
соответствующего однородного уравнения;
2) вычисление частного решения 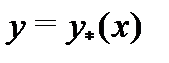 неоднородного уравнения (1).
неоднородного уравнения (1).
Самым трудным является осуществление первой процедуры. Однако для уравнений с постоянными коэффициентами (см. следующий раздел) ее можно всегда реализовать. Если же найдена фундаментальная система решений 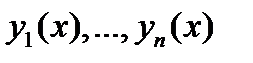 однородного уравнения
однородного уравнения 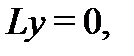 то реализовать вторую процедуру не составляет особого труда.
то реализовать вторую процедуру не составляет особого труда.
Теорема 2. Пусть 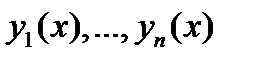 –- фундаментальная система решений однородного уравнения
–- фундаментальная система решений однородного уравнения 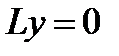 с непрерывными на отрезке
с непрерывными на отрезке 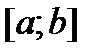 коэффициентами
коэффициентами 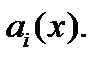 Если правая часть
Если правая часть 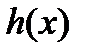 соответствующего неоднородного уравнения (1) непрерывна на отрезке
соответствующего неоднородного уравнения (1) непрерывна на отрезке 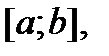 то его частное решение можно вычислить в виде
то его частное решение можно вычислить в виде
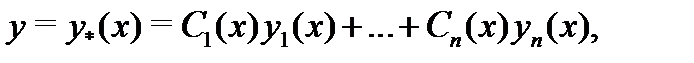
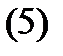
где функции 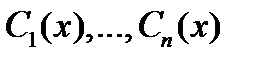 (представляющие собой варьированные постоянные общего решения однородного уравнения
(представляющие собой варьированные постоянные общего решения однородного уравнения 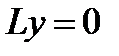 ) находятся из системы
) находятся из системы
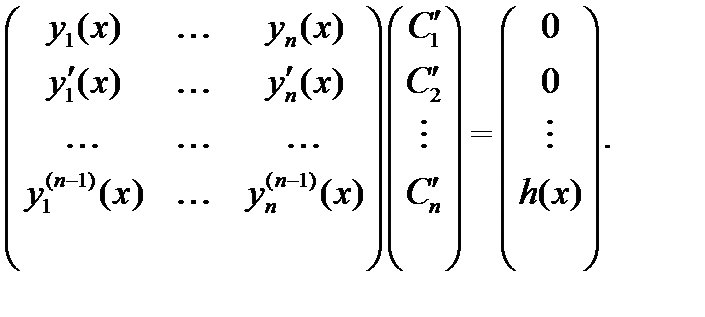
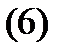
Доказательство. Проведем доказательство для уравнения второго порядка:
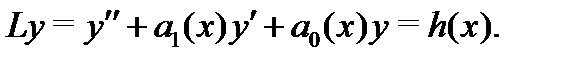
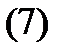
В этом случае система (6) имеет вид
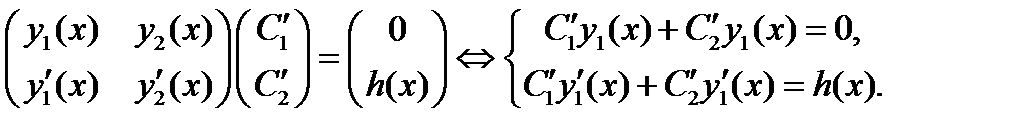
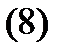
Проверим, что функция
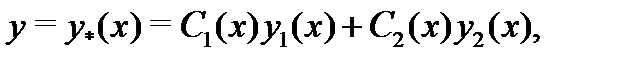
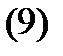
где 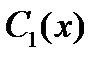 и
и 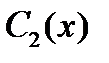 удовлетворяют уравнениям (8), является частным решением уравнения (7). Вычислим производные
удовлетворяют уравнениям (8), является частным решением уравнения (7). Вычислим производные 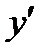 и
и 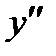 функции (9) с учетом равенств (8):
функции (9) с учетом равенств (8):
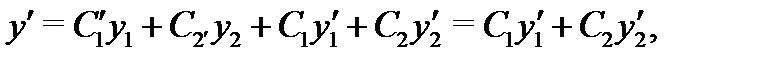
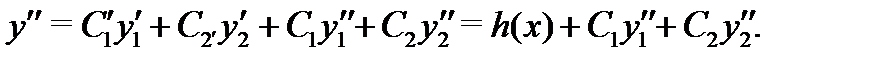
Отсюда получаем, что
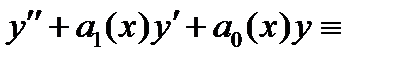
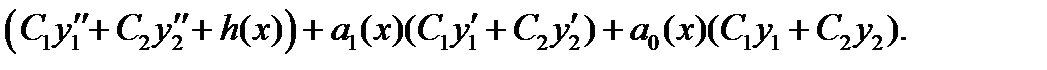
Группируя здесь коэффициенты отдельно перед каждой функций 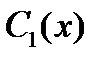 и
и 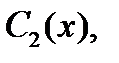 получаем
получаем
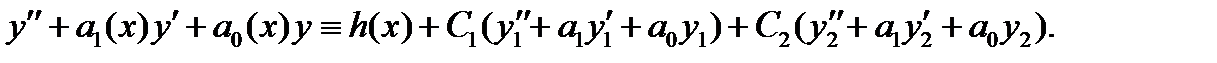
Поскольку 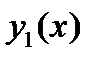 и
и 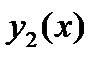 – решения соответствующего однородного уравнения
– решения соответствующего однородного уравнения 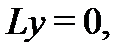 то
то 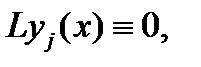 и значит
и значит 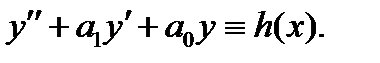 Таким образом, функция
Таким образом, функция 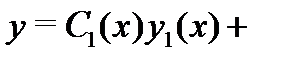
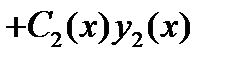 является частным решением неоднородного уравнения (7). Теорема доказана.
является частным решением неоднородного уравнения (7). Теорема доказана.
Пример 1. Проверить, что функции 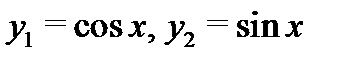 образуют фундаментальную систему решения уравнения
образуют фундаментальную систему решения уравнения 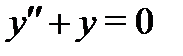 и найти общее решение неоднородного уравнения
и найти общее решение неоднородного уравнения 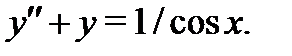
Решение.Поскольку 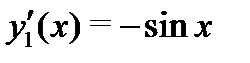 и
и 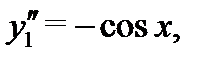 то функция
то функция 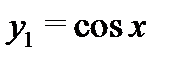 удовлетворяет уравнению
удовлетворяет уравнению 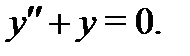 Точно так же убеждаемся, что функция
Точно так же убеждаемся, что функция 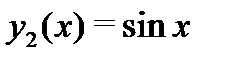 также удовлетворяет уравнению
также удовлетворяет уравнению 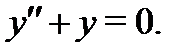 Вычисляем вронскиан
Вычисляем вронскиан
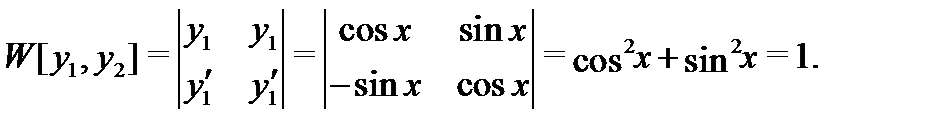
Видим, что он не обращается в нуль на промежутке 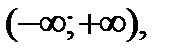 значит функции
значит функции 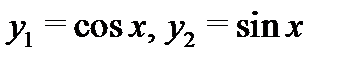 образуют фундаментальную систему решений уравнения
образуют фундаментальную систему решений уравнения 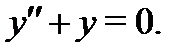
Найдем теперь частное решение 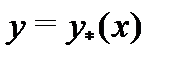 неоднородного уравнения
неоднородного уравнения 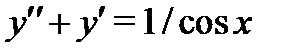 в форме
в форме 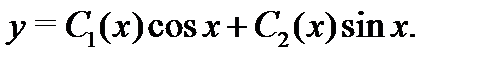 При этом функции
При этом функции 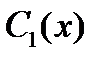 и
и 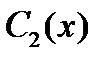 должны удовлетворять системе
должны удовлетворять системе
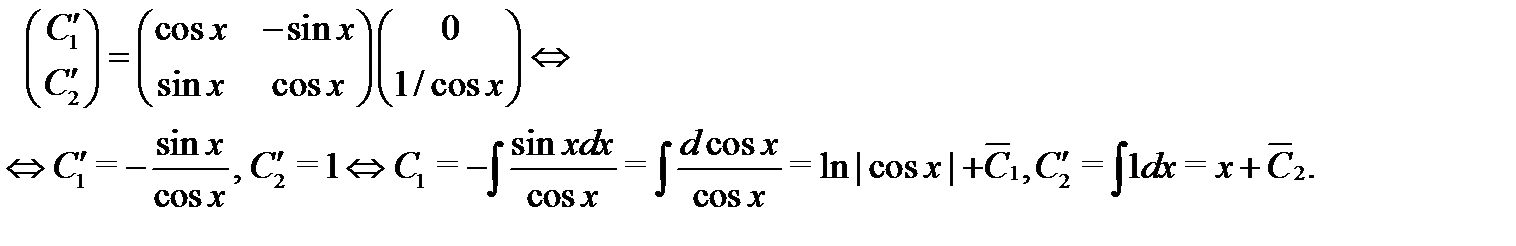
Поскольку нас интересует частное решение неоднородного уравнения 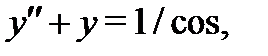 то
то 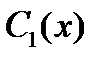 и
и 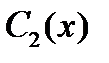 можно взять в виде
можно взять в виде 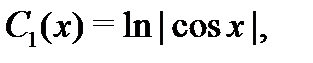
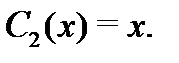 Подставляя их в функцию
Подставляя их в функцию 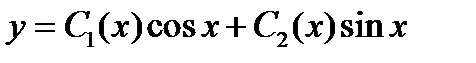 , получаем частное решение в виде
, получаем частное решение в виде
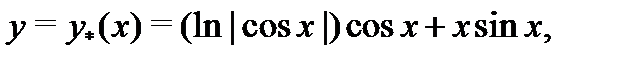
а значит, общее решение неоднородного уравнения запишется в форме
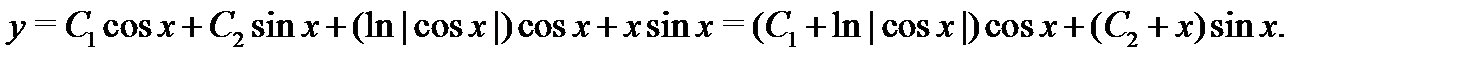
Дата добавления: 2016-06-05; просмотров: 2731;











