Свойства дифференциального оператора. Теорема Коши

Мы предполагаем, что читатель знаком с понятием линейного пространства и с основными его свойствами. В дальнейшем будут использоваться следующие пространства:

1) 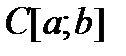– пространство функций, непрерывных на отрезке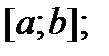

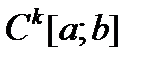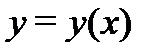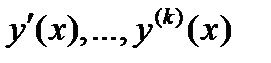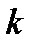2) – пространство функций непрерывных вместе со своими производными (до –го порядка включительно),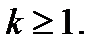

Эти пространства являются линейными пространствами с обычными для функций операциями сложения и умножения на числа.

Теорема 1. Если в операторе 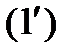все коэффициенты 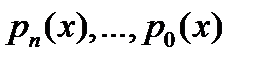непрерывны на отрезке 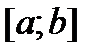, то 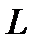действует из пространства 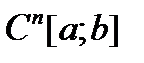в пространство 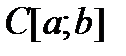(т.е. 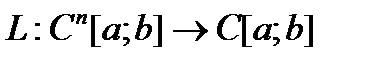) и является линейным оператором, т.е.

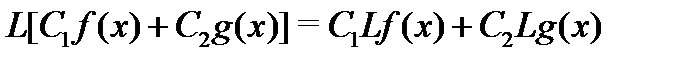
для произвольных постоянных 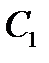и 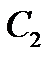и произвольных функций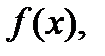

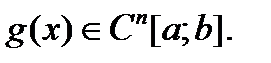
Действительно, при дифференцировании теряется гладкость функции на единицу, значит при 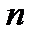–кратном дифференцировании функция класса 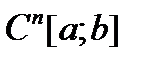переходит в функцию класса 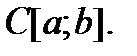Кроме того, поскольку операция дифференцирования линейна, то и линеен оператор 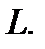Будем рассматривать в основном уравнения (1) со старшим коэффициентом 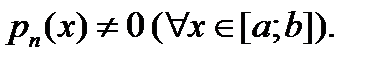B этом случае на него можно поделить уравнение (1) и записать его в форме

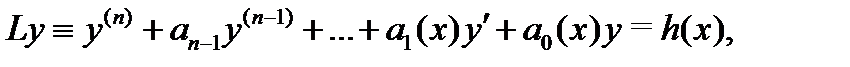
где обозначено:

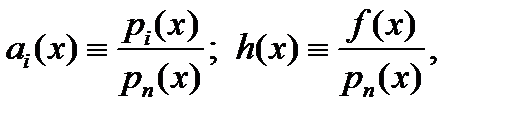
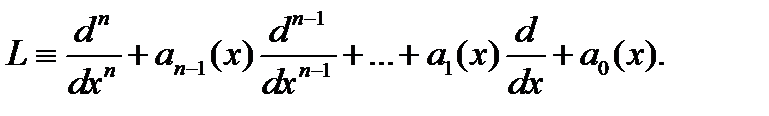
Наша ближайшая задача – изучить свойства решений этого уравнения. Начнем с теоремы существования и единственности решения задачи Коши

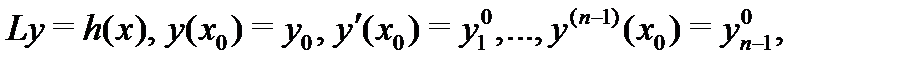
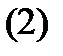
где 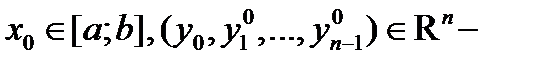произвольный вектор.

Теорема 2 (Коши) . Если в уравнении (2) все коэффициенты 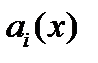и правая часть 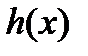непрерывны на отрезке 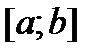, то задача Коши (2) для этого уравнения имеет единственное решение 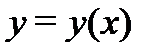и это решение определено также на этом отрезке.

Таким образом, теорема существования и единственности решения начальной задачи для линейного дифференциального уравнения носит "глобальный" характер в отличие от "локального" характера общей теоремы существования единственности решения для нелинейного уравнения.