Вычисление коэффициентов уравнения регрессии
Систему уравнений (7.8) на основе имеющихся ЭД однозначно решить невозможно, так как количество неизвестных всегда больше количества уравнений. Для преодоления этой проблемы нужны дополнительные допущения. Здравый смысл подсказывает: желательно выбрать коэффициенты полинома так, чтобы обеспечить минимум ошибки аппроксимации ЭД. Могут применяться различные меры для оценки ошибок аппроксимации. В качестве такой меры нашла широкое применение среднеквадратическая ошибка. На ее основе разработан специальный метод оценки коэффициентов уравнений регрессии – метод наименьших квадратов (МНК). Этот метод позволяет получить оценки максимального правдоподобия неизвестных коэффициентов уравнения регрессии при нормальном распределения вариант, но его можно применять и при любом другом распределении факторов.
В основе МНК лежат следующие положения:
· значения величин ошибок и факторов независимы, а значит, и некоррелированы, т.е. предполагается, что механизмы порождения помехи не связаны с механизмом формирования значений факторов;
· математическое ожидание ошибки ε должно быть равно нулю (постоянная составляющая входит в коэффициент a0), иначе говоря, ошибка является центрированной величиной;
· выборочная оценка дисперсии ошибки  должна быть минимальна.
должна быть минимальна.
Рассмотрим применение МНК применительно к линейной регрессии стандартизованных величин. Для центрированных величин uj коэффициент a0 равен нулю, тогда уравнения линейной регрессии
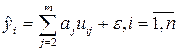 . (7.9)
. (7.9)
Здесь введен специальный знак "^", обозначающий значения показателя, рассчитанные по уравнению регрессии, в отличие от значений, полученных по результатам наблюдений.
По МНК определяются такие значения коэффициентов уравнения регрессии, которые обеспечивают безусловный минимум выражению
 . (7.10)
. (7.10)
Минимум находится приравниванием нулю всех частных производных выражения (7.10), взятых по неизвестным коэффициентам, и решением системы уравнений
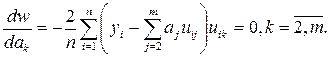 (7.11)
(7.11)
Последовательно проведя преобразования и используя введенные ранее оценки коэффициентов корреляции
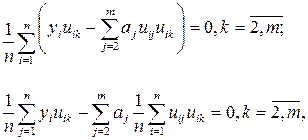
получим
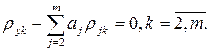 . (7.12)
. (7.12)
Итак, получено т–1 линейных уравнений, что позволяет однозначно вычислить значения a2, a3, …, aт.
Если же линейная модель неточна или параметры измеряются неточно, то и в этом случае МНК позволяет найти такие значения коэффициентов, при которых линейная модель наилучшим образом описывает реальный объект в смысле выбранного критерия среднеквадратического отклонения.
Когда имеется только один параметр, уравнение линейной регрессии примет вид
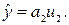
Коэффициент a2 находится из уравнения
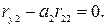
Тогда, учитывая, что r 2,2 = 1, искомый коэффициент
a2 = r y,2. (7.13)
Соотношение (7.13) подтверждает ранее высказанное утверждение, что коэффициент корреляции является мерой линейной связи двух стандартизованных параметров.
Подставив найденное значение коэффициента a2 в выражение для w, с учетом свойств центрированных и нормированных величин, получим минимальное значение этой функции, равное 1– r2y,2. Величину 1– r2y,2 называют остаточной дисперсией случайной величины y относительно случайной величины u2. Она характеризует ошибку, которая получается при замене показателя функцией от параметра υ= a2u2 . Только при |ry,2 | = 1 остаточная дисперсия равна нулю, и, следовательно, не возникает ошибки при аппроксимации показателя линейной функцией.
Переходя от центрированных и нормированных значений показателя и параметра
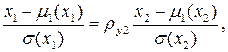
можно получить для исходных величин
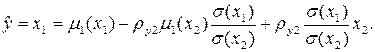 (7.14)
(7.14)
Это уравнение также линейно относительно коэффициента корреляции. Нетрудно заметить, что центрирование и нормирование для линейной регрессии позволяет понизить на единицу размерность системы уравнений, т.е. упростить решение задачи определения коэффициентов, а самим коэффициентам придать ясный смысл.
Применение МНК для нелинейных функций практически ничем не отличается от рассмотренной схемы (только коэффициент a0 в исходном уравнении не равен нулю).
Например, пусть необходимо определить коэффициенты параболической регрессии
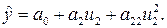
Выборочная дисперсия ошибки
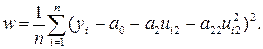
 На ее основе можно получить следующую систему уравнений
На ее основе можно получить следующую систему уравнений
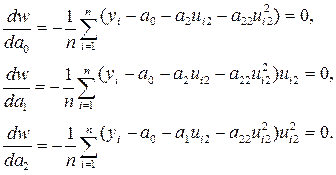
После преобразований система уравнений примет вид

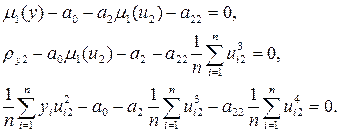
Учитывая свойства моментов стандартизованных величин, запишем
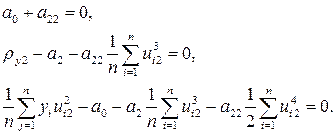
Определение коэффициентов нелинейной регрессии основано на решении системы линейных уравнений. Для этого можно применять универсальные пакеты численных методов или специализированные пакеты обработки статистических данных.
С ростом степени уравнения регрессии возрастает и степень моментов распределения параметров, используемых для определения коэффициентов. Так, для определения коэффициентов уравнения регрессии второй степени используются моменты распределения параметров до четвертой степени включительно. Известно, что точность и достоверность оценки моментов по ограниченной выборке ЭД резко снижается с ростом их порядка. Применение в уравнениях регрессии полиномов степени выше второй нецелесообразно.
Качество полученного уравнения регрессии оценивают по степени близости между результатами наблюдений за показателем и предсказанными по уравнению регрессии значениями в заданных точках пространства параметров. Если результаты близки, то задачу регрессионного анализа можно считать решенной. В противном случае следует изменить уравнение регрессии (выбрать другую степень полинома или вообще другой тип уравнения) и повторить расчеты по оценке параметров.
При наличии нескольких показателей задача регрессионного анализа решается независимо для каждого из них.
Анализируя сущность уравнения регрессии, следует отметить следующие положения. Рассмотренный подход не обеспечивает раздельной (независимой) оценки коэффициентов – изменение значения одного коэффициента влечет изменение значений других. Полученные коэффициенты не следует рассматривать как вклад соответствующего параметра в значение показателя. Уравнение регрессии является всего лишь хорошим аналитическим описанием имеющихся ЭД, а не законом, описывающим взаимосвязи параметров и показателя. Это уравнение применяют для расчета значений показателя в заданном диапазоне изменения параметров. Оно ограниченно пригодно для расчета вне этого диапазона, т.е. его можно применять для решения задач интерполяции и в ограниченной степени для экстраполяции.
Главной причиной неточности прогноза является не столько неопределенность экстраполяции линии регрессии, сколько значительная вариация показателя за счет неучтенных в модели факторов. Ограничением возможности прогнозирования служит условие стабильности неучтенных в модели параметров и характера влияния учтенных факторов модели. Если резко меняется внешняя среда, то составленное уравнение регрессии потеряет свой смысл. Нельзя подставлять в уравнение регрессии такие значения факторов, которые значительно отличаются от представленных в ЭД. Рекомендуется не выходить за пределы одной трети размаха вариации параметра как за максимальное, так и за минимальное значения фактора.
Прогноз, полученный подстановкой в уравнение регрессии ожидаемого значения параметра, является точечным. Вероятность реализации такого прогноза ничтожна мала. Целесообразно определить доверительный интервал прогноза. Для индивидуальных значений показателя интервал должен учитывать ошибки в положении линии регрессии и отклонения индивидуальных значений от этой линии. Средняя ошибка прогноза показателя y для фактора х составит
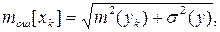
где 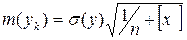 – средняя ошибка положения линии регрессии в генеральной совокупности при x = xk;
– средняя ошибка положения линии регрессии в генеральной совокупности при x = xk;
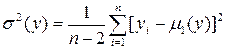 – оценка дисперсии отклонения показателя от линии регрессии в генеральной совокупности;
– оценка дисперсии отклонения показателя от линии регрессии в генеральной совокупности;
xk – ожидаемое значение фактора.
Доверительные границы прогноза, например, для уравнения регрессии (7.14), определяются выражением 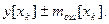
Отрицательная величина свободного члена а0 в уравнении регрессии для исходных переменных означает, что область существования показателя не включает нулевых значений параметров. Если же а0 > 0, то область существования показателя включает нулевые значения параметров, а сам коэффициент характеризует среднее значение показателя при отсутствии воздействий параметров.
Задача 7.2. Построить уравнение регрессии для пропускной способности канала по выборке, заданной в табл. 7.1.
Решение. Применительно к указанной выборке построение аналитической зависимости в основной своей части выполнено в рамках корреляционного анализа: пропускная способность зависит только от параметра "соотношение сигнал/шум". Остается подставить в выражение (7.14) вычисленные ранее значения параметров. Уравнение для пропускной способности примет вид
ŷ= 26,47– 0,93×41,68×5,39/6,04+0,93×5,39/6,03×х = – 8,121+0,830х.
Результаты расчетов представлены в табл. 7.5.
Таблица 7.5
| N пп | Пропускная способность канала | Соотношение сигнал/шум | Значение функции | Погрешность |
| Y | X | ŷ | ε | |
| 26.37 | 41.98 | 26.72 | -0.35 | |
| 28.00 | 43.83 | 28.25 | -0.25 | |
| 27/83 | 42.83 | 27.42 | 0.41 | |
| 31.67 | 47.28 | 31.12 | 0.55 | |
| 23.50 | 38.75 | 24.04 | -0.54 | |
| 21.04 | 35.12 | 21.03 | 0.01 | |
| 16.94 | 32.07 | 18.49 | -1.55 | |
| 37.56 | 54.25 | 36.90 | 0.66 | |
| 18.84 | 32.70 | 19.02 | -0.18 | |
| 25.77 | 40.51 | 25.50 | 0.27 | |
| 33.52 | 49.78 | 33.19 | 0.33 | |
| 28.21 | 43.84 | 28.26 | -0.05 | |
| 28.76 | 44.03 | 28.42 | 0.34 | |
| 24.60 | 39.46 | 24.63 | -0.03 | |
| 24.51 | 38.78 | 24.06 | 0.45 |
Остаточная дисперсия стандартизованной величины Y относительно37.56 стандартизованной величины Х равна 1– 0,932 = 0,14, т.е. является малой величиной. Погрешность аппроксимации и величина остаточной дисперсии показывают высокую точность линейной модели, поэтому задачу регрессионного анализа можно считать решенной. Свободный член уравнения регрессии отрицательный, следовательно, область существования показателя не включает нулевое значение параметра "отношение сигнал/шум", что вытекает из сущности параметра (при нулевом уровне сигнала передача информации невозможна).
Дата добавления: 2022-02-05; просмотров: 393;











