ЗАКОН РАСПРЕДЕЛЕНИЯ НЕРНСТА–ШИЛОВА. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА РАСПРЕДЕЛЕНИЯ
Для получения материалов с определенными и контролируемыми свойствами исходные компоненты подвергают различным методам очистки. Наиболее эффективные методы очистки, осуществляемые при фазовых превращениях исходных веществ из одного агрегатного состояния в другое, основаны на различной растворимости компонентов системы (примесей) в двух равновесных фазах. Это различие количественно характеризуется коэффициентом распределения – отношением активностей (концентраций) данного компонента в сосуществующих равновесных фазах.
Этот пример является частным случаем общей закономерности, которая носит название закона распределения Нернста–Шилова: отношение активностей (концентраций) вещества, распределяющегося между двумя несмешивающимися жидкостями или газами, является при каждой данной температуре величиной постоянной. В растворах или гетерогенных системах, состоящих из двух и более компонентов, изменение состава (вследствие химических реакций, испарения, конденсации, фазовых переходов компонента из одной фазы в другую и т. д.) влияет на условия существования каждого компонента и соответственно на их термодинамические свойства. Для характеристики состояния компонента в фазе данного состава при определенных внешних условиях в термодинамике используют понятие химического потенциала μ. Эта величина определяется равенством
 (5.1)
(5.1)
и представляет собой частную производную свободной энергии Гиббса по числу молей К – компонента при постоянных давлении, температуре и числу молей остальных компонентов.
Численно химический потенциал компонента μK равен приращению свободной энергии Гиббса системы при добавлении одного моля этого компонента к такому большому объема системы, что при P и T = const состав ее практически не изменяется. В отличие от свободной энергии Гиббса, которая характеризует отдельный компонент или систему в целом, химический потенциал характеризует компонент, входящий в состав системы и испытывающий воздействие всех остальных компонентов.
Изменение свободной энергии Гиббса всей системы равно сумме произведений числа молей каждого компонента на его химический потенциал, т.е.
∂G = ∑μK dnK. (5.2)
Если в гетерогенной системе происходит самопроизвольное перераспределение компонентов между фазами, то ∂G < 0 и неравенство
∑μK dnK < 0 (5.3)
выражает общее условие возможности протекания процессов в открытых системах.
Из выражения (3.3) следует, что компонент будет переходить самопроизвольно из фазы (1), где он имеет более высокий химический потенциал, в фазу (2), где его химический потенциал ниже, т. е.
μKI > μKII. (5.4)
Такой переход сопровождается уменьшением химического потенциала в первой фазе и увеличением его во второй фазе.
При достижении равновесия химические потенциалы данного компонента в обеих фазах при данной температуре равны между собой, т.е.
μKI = μKII. (5.5)
При этом его равновесные активности (концентрации) в обеих фазах остаются неизменными.
Химический потенциал зависит от природы веществ, их активностей (концентраций), от температуры и от давления (для газообразных веществ).
Зависимость химического потенциала компонента от концентрации выражается уравнением
μK = μK0 + RT·ln(cK) , (5.6)
где cK – концентрация компонента в данной фазе, моль/л или экв/л; μK0 – стандартный химический потенциал компонента в данной фазе при 298 К, зависящий от природы компонента и природы фазы.
Исходя из уравнений (5.5) и (5.6) для двух равновесных фаз запишем
μ K0(1) + RT·ln(cK(1))= μ K0(2) + RT·ln(cK(2)) , (5.7)
при этом μ K0(1) ≠ μ K0(2) и при T = const являются величинами постоянными, тогда
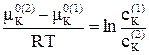 . (5.8)
. (5.8)
Так как все члены, входящие в левую часть уравнения, постоянны, то
 или
или  , (5.9)
, (5.9)
где K – термодинамическая константа (коэффициент) распределения. Выражение (5.9) является математической записью закона Нернста–Шилова.
Если распределяемый компонент диссоциирует или ассоциирует в данных фазах, то выражение (5.9) принимает вид
 , (5.10)
, (5.10)
где α1 и α2 – степени диссоциации или ассоциации компонента в первой и второй фазах соответственно.
Численное значение коэффициента распределения K зависит от природы равновесных фаз, природы распределяемого между ними компонента, от температуры и не зависит от относительного количества равновесных фаз и исходной концентрации распределяемого компонента.
Закон распределения Нернста–Шилова находит широкое применение в решении разнообразных практических задач.
Экстракцией называется физический процесс разделения гомогенной смеси (раствора) двух и более веществ на составляющие компоненты с помощью вспомогательного растворителя – экстрагента, добавление которого вызывает расслаивание раствора. Экстрагент выбирается с таким расчетом, чтобы он не смешивался с исходным раствором и хорошо растворял в себе экстрагируемый компонент. При этом экстрагирование будет тем полнее, чем больше коэффициент распределения отличается от единицы. Например, экстрагентом для извлечения иода из воды может служить четыреххлористый углерод (CCl4), коэффициент распределения при этом равен
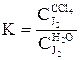 .
.
Следует заметить, что полноту экстрагирования можно увеличить, если имеющийся запас экстрагента использовать по частям, учитывая, что все процессы идут до установления равновесия.
Извлечение вещества жидкостью из жидкости называется жидкостной экстракцией, газа жидкостью или твердой фазой – газовой абсорбцией, твердого вещества жидкостью – выщелачиванием.
Различная растворимость примесей в расплаве и соприкасающейся с ним твердой фазе количественно характеризуется коэффициентом сегрегации Kc:
KC = CS/CL, (5.11)
где CS – концентрация примеси в твердой фазе; CL – концентрация примеси в жидкой фазе (расплаве).
Например, при очистке полупроводниковых материалов от примесей методами направленной кристаллизации расплава или зонной плавки примеси, для которых KC < 1 (Al, Ga в Ge: KC = 0,01; In в Ge: KC = 0,001; Те и Bi в Ge: KC = 4·10–5), концентрируются в зоне расплава, а в зоне кристаллизации образуется слой вещества более чистого относительно указанных примесей. При этом чем меньше единицы значение коэффициента сегрегации, тем эффективнее очистка от примесей.
Примеси, для которых KC > 1 (В в Ge: KC = 17,3), концентрируются в твердой фазе, и эти методы очистки малоэффективны.
Очистка от примесей с KC = 1 практически невозможна, например В в Si: KC = 1.
Учитывая исходные концентрации примеси в начальном участке очищаемого вещества и характер распределения ее по слитку, а также значение коэффициента сегрегации, можно получить материал с равномерным распределением примеси по слитку образца. Так, если в расплавленную зону германия ввести легирующую примесь с KC > 1, например Zn, то прохождением зоны расплава вдоль всего слитка можно достигнуть равномерного распределения примеси и получить материал с дырочным механизмом проводимости.
Следует заметить, что по данным зонной плавки или направленной кристаллизации можно определить численное значение коэффициента сегрегации. Для этого слиток после очистки делят на равные части и в каждой аналитически определяют концентрацию исследуемой примеси. Зная первоначальное содержание примеси в материале, вычисляют коэффициент сегрегации.
Коэффициент сегрегации можно определить, используя диаграммы плавкости основного вещества и компонента-примеси как отношение концентрации примеси в твердой фазе CS (проекция точки пересечения изотермы с линией солидус на ось составов) к концентрации примеси в жидкой фазе (расплаве) CL (проекция точки пересечения изотермы с линией ликвидус на ось составов) при заданной температуре.
Порядок выполнения опыта. Приготовьте из четыреххлористого углерода, 0,05 н раствора иода в четыреххлористом углероде и воды смеси различных составов. Для этого отмерьте с помощью мерного цилиндра необходимые количества каждого из компонентов, как указано в табл. 5.1, и поместите в мерные колбы емкостью 200–250 мл.
Таблица 5.1
Составы исследуемых смесей
| Номер смеси | Объем 0,05 н раствора I2 в четыреххлористом углероде ССl4, мл | Объем четыреххлористого углерода ССl4, мл | Объем воды, мл |
Закройте колбы плотно пробками и с помощью магнитной мешалки перемешайте содержимое в течение 30–40 мин. Отключите мешалку и оставьте колбы на 10–20 мин отстаиваться для расслоения жидкостей. Затем содержимое колбы со смесью №1 перелейте в делительную воронку для отделения органического слоя от неорганического (водного). Слейте органический слой (окрашенный в фиолетовый цвет) в пронумерованный стакан №1, водный – в стакан №2.
Примечание: при проведении опытов ССl4 может быть заменен на гексан.
Концентрацию иода в экв/л (нормальность) определяют титрованием смесей растворами гипосульфита натрия. При этом протекает следующая окислительно-восстановительная реакция:
2Na2S2O3 + I2 = Na2S4O6 + 2NaI.
Для установления точки эквивалентности указанную реакцию проводят в присутствии крахмала, который является индикатором на I2.
Заполните две бюретки для титрования растворами гипосульфита натрия различных концентраций: 0,05 н и 0,001 н.
Определите концентрацию иода в органическом слое: для этого из стакана №1 с помощью мерного цилиндра возьмите 2 мл смеси, перенесите в коническую колбу для титрования, добавьте 25 мл дистиллированной воды (гипосульфитом можно титровать только водный раствор) и несколько капель крахмала (индикатор на I2). Постепенно, по каплям добавляя из бюретки 0,05 н раствор гипосульфита натрия, оттитруйте содержимое конической колбы до обесцвечивания раствора. В процессе титрования колбу все время встряхивайте, чтобы иод постепенно внедрялся в водную часть раствора. Определите объем раствора гипосульфита, использованного для титрования, и запишите в табл. 5.2.
Каждуюсмесь титруйте не менее трех раз (до получения трех близких по значениям результатов), взяв для расчета среднее значение объема гипосульфита, использованного для титрования.
Определите концентрацию иода в водном слое: из стакана №2 с помощью мерного цилиндра возьмите 20–25 мл смеси, перенесите в коническую колбу для титрования и добавьте несколько капель крахмала. Оттитруйте содержимое конической колбы 0,001 н раствором гипосульфита натрия, соблюдая все вышеуказанные условия титрования. Определите объем раствора гипосульфита, использованного для титрования водного слоя, и запишите в табл. 5.2.
Повторите эксперимент для составов № 2, 3, 4. Результаты эксперимента и данные опыта занесите в табл. 5.2.
Так как концентрация растворов гипосульфита натрия выражена через нормальность (экв/л), то для расчета концентрации иода в титруемой смеси используйте закон эквивалентов: объемы реагирующих веществ обратно пропорциональны их нормальностям. Тогда
 , (5.12)
, (5.12)
где Vсмеси – объемы титруемых смесей, органического и водного слоев соответственно, мл; 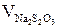 – объемы гипосульфита, использованные для титрования органического и водного слоев, соответственно мл;
– объемы гипосульфита, использованные для титрования органического и водного слоев, соответственно мл; 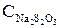 – концентрации (нормальности) иода в органическом или водном слоях, экв/л;
– концентрации (нормальности) иода в органическом или водном слоях, экв/л;  – концентрация (нормальность) растворов гипосульфита, используемых на титрование; для органического слоя
– концентрация (нормальность) растворов гипосульфита, используемых на титрование; для органического слоя 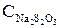 = 0,05 н, для водного
= 0,05 н, для водного 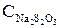 = 0,001 н.
= 0,001 н.
Таблица 5.2
Форма записи результатов опыта
| Номер смеси | Органический слой CCl4 | Водный слой | Значение K | ||||
| Объем титруемой смеси, V1, мл | Объем 0,05 н Na2S2O3, использ. на титр. V2, мл | Концентрация J2 в органическом слое 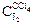 , экв./л , экв./л
| Объем титруемой смеси, V3, мл | Объем 0,001 н Na2S2O3, использ. на титр. V4, мл | Концентрация J2 в водном слое 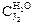 , экв./л , экв./л
| ||
При выполнении анализа результатов опыта выполните задания и ответьте на вопросы:
1. Рассчитайте для всех исследуемых смесей концентрации иода в четыреххлористом углероде ( ), пользуясь данными табл. 5.2 и соотношением 5.12.
 , экв./л. V1 = 2 мл (5.13)
, экв./л. V1 = 2 мл (5.13)
Данные занесите в табл. 5.2.
2. Рассчитайте для всех исследуемых смесей концентрации иода в водном слое:
 , экв./л. V3 = 20 – 25 мл (5.14)
, экв./л. V3 = 20 – 25 мл (5.14)
Данные запишите в табл. 5.2.
3. По полученным данным рассчитайте коэффициент распределения иода между двумя несмешивающимися жидкостями (вода – четыреххлористый углерод), используя соотношение (5.9):
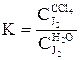 .
.
4. Сравните коэффициенты распределения для всех смесей и установите, зависит ли коэффициент распределения от концентрации раствора. Сделайте вывод, указав, что установлено в результате выполнения опыта. В каких случаях четыреххлористый углерод может быть использован в качестве экстрагента? Ответы должны быть полными и обоснованными.
ЛИТЕРАТУРА
1. Краткий курс физической химии : учеб. пособие для вузов / под ред. С. Н. Кондратьева. – М. : Высш. шк., 1978.
2.Голиков, Г. А. Руководство по физической химии : учеб. пособие для вузов / Г. А. Голиков. – М. : Высш. шк., 1988.
3.Угай, Я. А. Введение в химию полупроводников : учеб. пособие для вузов / Я. А. Угай. – М. : Высш. шк. 1989.
Дата добавления: 2022-02-05; просмотров: 1023;











