НОК целых чисел и его вычисление
Определение 8.4.Общим кратным конечного множества целых чисел a1, a2,…, ak, отличных от нуля, называют целое число m, которое делится на все числа аi (i = 1, 2, … , k).
Определение 8.5.Целое число m называется наименьшим общим кратным чисел a1, a2, …, аk , отличных от нуля, если:
1.m – является их общим кратным;
2. m делит любое другое общее кратное этих чисел.
Обозначение: m = НОК(a1, a2, …, аk) или m = [a1, a2, …, аk].
Теорема 8.6. Наименьшее общее кратное целых чисел а и b определяется однозначно с точностью до знака.
Действительно, если предположить, что m1 = [a, b] 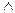 m2 = [a, b], то m1
m2 = [a, b], то m1 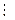 m2
m2 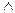 m2
m2 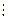 m1, поэтому m1 = m2
m1, поэтому m1 = m2 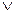 m2 = - m1.
m2 = - m1.
Замечание.Обычно берется положительное значение [a, b] .
Пример. Даны числа 3, 4, 6, 8. Числа 24, 48, 96 являются общими кратными чисел 3, 4, 6, 8. Наименьшим общим кратным будет число 24. [24, 48, 96] = 24.
Между наименьшим общим кратным и наибольшим общим делителем двух целых чисел существует зависимость, которая выражается формулой:
[a, b] = 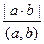
Эта связь позволяет утверждать, что для любой пары целых чисел, отличных от нуля, существует наименьшее общее кратное.
Пример.1.Вычислим НОК [154, 48] = 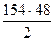 = 3696.
= 3696.
2. Наиболее просто НОД двух целых чисел вычисляется в том случае, когда (а, b) = 1, тогда [a, b] = 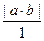 = | a ∙ b |. Например,
= | a ∙ b |. Например,
[21, 5] = 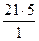 = 105.
= 105.
Дата добавления: 2021-12-14; просмотров: 606;











