Основные газовые законы и уравнение состояния

Закон Бойля-Мариотта (1662). Роберт Бойль нашел, что при Т=const объем данного количества газа пропорционален давлению, под которым он находится. Рассмотрим переход газа массой m из состояния 1 (Р₁V₁Т) в состояние 2 (Р₂V₂Т) при постоянной температуре Т (изотермический процесс). По закону Бойля Р₁V₁ = Р₂V₂ = Р₃V₃ …, т.е. РV = const.

Графически этот закон можно представить в координатах «РV – Р» прямой, параллельной оси давлений, а в координатах Р и V – ветвью гиперболы. Этот закон дает простой метод прогнозирования объема газов при изменении давления, оказываемого на них, с хорошим приближением для большинства газов кроме случаев, когда Т низкая и Р высокое.

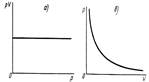
Рисунок 1. Графическое изображение закона Бойля-Мариотта

Пример. 1 моль газа занимает объем 24 дм³ при комнатной температуре и давлении 1 атм. Каким станет этот объем, если увеличить давление до 15 атм?

Решение. P₁V₁ = P₂V₂; (1 атм) ∙ (24 дм³) = (15 атм) ∙ (Х дм³); Х = 1,6 дм³.

Закон Шарля.Рассмотрим переход газа массой m из состояния 1 (Т₁V₁Р) в состояние 2 (Т₂V₂Р) при постоянном давлении (изобарный процесс).

Экспериментальным путем Шарль установил, что при этом объем газа линейно изменяется с температурой. Коэффициент пропорциональности равен 1/273,16. Это значит, что при каждом повышении температуры на 1 градус объем газа возрастает на 1/273,16 его первоначального значения. Было также показано, что V₂/T₂ = V₁/T₁ = const, т.е. отношение объема к абсолютной температуре при постоянном давлении постоянно:

V/ T = const:

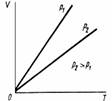
Рисунок 2. Графическое изображение закона Шарля

Закон Гей-Люссака. Рассмотрим переход газа массой m из состояния 1 (Т₁VР₁) в состояние 2 (Т₂VР₂) при постоянном объеме (изохорныйпроцесс).

При этом давление газа линейно изменяется с температурой с тем же коэффициентом пропорциональности. Т.о, при повышении Т на один градус давление газа увеличивается на 1/273,16 первоначального значения. Было также показано, что p₂/T₂ = p₁/T₁ = const, т.е. отношение давления к абсолютной температуре при постоянном объеме постоянно:

P/T = const.

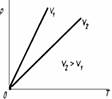
Рисунок 3. Графическое изображение закона Гей-Люссака

Закон Дальтона. Если в ограниченном пространстве объема V смешать несколько идеальных газов, то каждый газ будет оказывать свое собственное давление, называемое парциальным (т.е. такое, как если бы газ в одиночку занимал весь объем). Общее наблюдаемое давление будет равно сумме парциальных давлений каждого газа.

Этот закон выводится из уравнения состояния идеального газа. Допустим, что в ограниченном объеме V при температуре Т содержится смесь идеальных газов А, В, С, количество вещества (молей) которых равно соответственно n_A, n_B, n_C. Общее измеренное давление составляет р_общ. Тогда давление смеси газов определяется суммой молей n_A+ n_B + n_C при температуре Т, объеме V и давлении р_общ.

Используя уравнение состояния, получим:

р_общ= (n_A+ n_B + n_C)RT

Если n_A молекул А занимают весь объем V при температуре Т, газ А оказывает давление р_А, которое является парциальным давлением газа А в смеси.

Запишем уравнение состояния газа А:

р_АV = n_A RT.

Таким же образом для газов В и С имеем:

р_ВV = n_ВRT, р_СV = n_СRT.

Суммирование этих трех уравнений дает соотношение:

(р_А +р_В +р_С) = (n_A+ n_B + n_C)∙RT

При сравнении (1) и (2) получим:

р_общ= р_А +р_В +р_С =Σ парциальных давлений = n_общ.

Из приведенных уравнений можно легко получить значение молярной доли, показывающей, какую часть от общего количества (молей) смеси составляет данный газ. Например, для газа А парциальное давление равно р_А = n_A RT/V, а для суммы газов р_общ = n_общ RT/V.

Поделив одно равенство на другое, получим:

р_А /P_общ = n_A / n_общ = Х_А,

где Х_А – молярная доля газа А; Х_В и Х_С – соответственно молярные доли газов В и С.

Естественно, сумма молярных долей всех газов, входящих в данную смесь, равна единице, т.е. для рассматриваемого случая Х_А + Х_В +Х_С =1.