Структурная формула плоского механизма

В плоском механизме для соединения звеньев можно использовать только плоские кинематические пары четвертого и пятого классов
(рис. 1.4 и рис. 1.5).

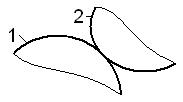
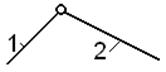
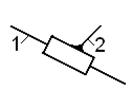
Пара IV класса	Пары V класса
а – вращательная	б –поступательная
Рис. 1.4	Рис. 1.5

Пусть плоский механизм состоит из n подвижных звеньев; для соединения их между собой и для их присоединения к стойке использовано 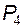пар четвертого и 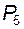пар пятого классов.

Если на движение звена в плоскости не наложено никаких условий связи, то оно обладает тремя степенями свободы; следовательно, все подвижные звенья имеют (до их соединения кинематическими парами) 3n степеней свободы; каждая пара четвертого класса является двухподвижной, т.е. из трех возможных относительных движений изымает одно; аналогично, каждая пара пятого класса является одноподвижной и из трех возможных движений изымает два. Тогда степень подвижности плоского механизма (или его число степеней свободы относительно стойки)

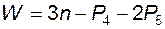. (1.1)

Таким образом, нами получена структурная формула П. Л. Чебышева (впервые выведена им в 1869 г.).

При расчете степени подвижности механизма по формуле (1.1) необходимо учитывать следующие, нередко встречающиеся ситуации:

1) наличие кратных шарниров; так, соединение звеньев, показанное на рис. 1.6, необходимо считать как два шарнира, иначе расчет по (1.1) даст завышенное значение W;

2) наличие местных подвижностей, т.е. таких, устранение которых не повлияет на кинематику механизма; у механизма по рис. 1.3 при любом положении кулачка 1 коромысло 3 может занимать только одно (единственно возможное) положение; следовательно, у этого механизма заведомо W=1, однако расчет по формуле (1.1) приводит к явно завышенному значению

;

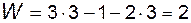для получения достоверного результата нужно ролик 2 мысленно объединить с коромыслом 3 в одно звено (рис. 1.7, б), тогда фактическая подвижность механизма

.

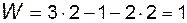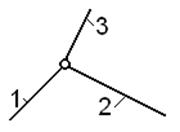Двойной шарнир Рис. 1.6

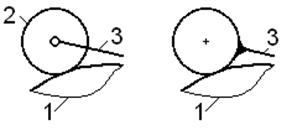а б Устранение местной подвижности Рис. 1.7

Отметим, что эти действия корректны только при круглом ролике, у которого геометрический центр совпадает с центром шарнира;

3)наличие пассивных (или избыточных) связей.

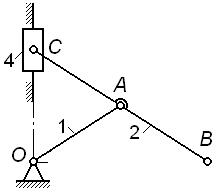
На рис. 1.8, а – г показаны четыре варианта исполнения механизма эллипсографа (длины звеньев ).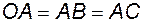

Анализ кинематических свойств этих схем показывает следующее:

· у механизма по рис. 1.8, а подвижность 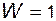, траектория точки B – горизонтальная прямая; следовательно, без ущерба для подвижности и кинематики механизма допускается включение в его схему ползуна 3 (как в
схеме по рис. 1.8, г);

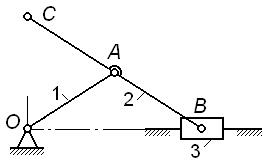
· аналогично у механизма по рис. 1.8, б также 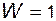, а траектория точки C – вертикальная прямая и его схему можно заменить той же схемой 1.8, г постановкой ползуна 4;

а)	б)
в)	г)
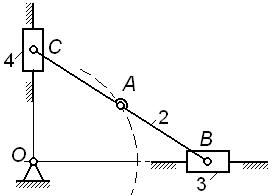
Рис. 1.8

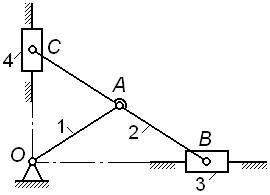
· у механизма по рис. 1.8, в степень подвижности 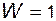и траектория точки A – окружность радиуса OA;, следовательно, без ущерба для подвижности и кинематики механизма в его схему можно включить кривошип 1 длиной 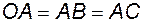, как в схеме по рис. 1.8, г.

ПодытоживаяПодытоживая, заключаем, что механизм по рис. 1.8, г кинематически эквивалентен любому из трех остальных механизмов; однако расчет по формуле (1.1) приводит к заведомо заниженному результату

,

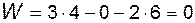т.е. формально – это не механизм, а ферма, что противоречит фактам. В таких случаях говорят, что механизм имеет избыточные или пассивные связи, которые, хотя и присутствуют в механизме, не влияют на его кинематику.

От пассивных связей при структурном анализе механизмов следует избавляться: в данном случае, в зависимости от смысла решаемой задачи, цель достигается удалением одного из звеньев – 1, 3 или 4 (вместе с соответствующим кинематическими парами). Тогда

,

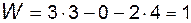что соответствует истине.