Замена высших кинематических пар низшими
 а)
а)
| б) 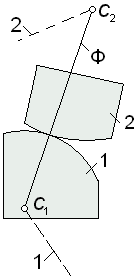
|
| Принцип построения заменяющих схем | |
| Рис. 1.9 |
Для любого плоского механизма, содержащего вы-сшие кинематические пары, можно построить так называемый заменяющий механизм, который не содержит высших пар, но эквивалентен заменяемому механизму по следующим показателям:
1) в структурном отношении (имеет ту же подвижность);
2) в отношении кинематики (при тех же законах движения входных звеньев остаются прежними законы движения выходных, сохраняются также траектории и законы движения всех точек);
3) в силовом отношении.
Если высшая пара образована профилями переменной кривизны, то вместо термина «заменяющий» используют «мгновенно-заменяющий».
имеет туопускается включение в его схему ползуна 3, как в
схеме по рис. 1.8, г;
одноименные размеры звеньев у всех вариантов схем одинаковы, кинематические свойства – сопоставимы, фактическая степень подвижности для каждой из схем 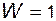 .
.
и движется Однако, расчет числа степеней свободы для механизма по
рис. 1.8, а приводит к за ниженному результату
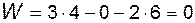 ;
;
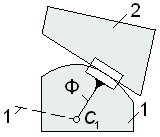
формально – это не механизм, а ферма; для остальных вариантов схем расчет приводит к правильному результату 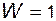 , т.е. изъятие из механизма любого из звеньев 4, 3 или 1. Как видно, не нарушая основных кинематических свойств механизПри выполнении процедуры замены каждой высшей пары вводится так называемое фиктивное звено (на рис. 1.9 обозначено буквой Ф), участвующее в двух парах пятого класса: либо в поступательной и вращательной (если один из профилей – прямая), либо в двух вращательных парах.
, т.е. изъятие из механизма любого из звеньев 4, 3 или 1. Как видно, не нарушая основных кинематических свойств механизПри выполнении процедуры замены каждой высшей пары вводится так называемое фиктивное звено (на рис. 1.9 обозначено буквой Ф), участвующее в двух парах пятого класса: либо в поступательной и вращательной (если один из профилей – прямая), либо в двух вращательных парах.
Центры шарниров фиктивных звеньев всегда совпадают с центрами кривизны контактирующих профилей.
1.5. ма по рис. 1.8, а, можно у с соответствующими кинематическими парами; при этом
Классификация плоских механизмов
по Л. В. Ассуру
Замечено, что к любому плоскому механизму можно присоединить такую кинематическую цепь, что степень его подвижности не изменится. Если эта цепь является кратчайшей (т.е. не распадается на более короткие и обладающие тем же свойством), и если при ее формировании использованы только низшие пары пятого класса, то такую цепь называют структурной группойили группой Ассура (в дальнейшем – просто группой). При наличии в механизме высших пар от них всегда можно избавиться с помощью описанной выше процедуры замены.
Из сказанного следует, что группа, присоединенная к стойке, имеет нулевую подвижность, но тогда она является и кинематически и статически определимой системой.
Пусть группа состоит из n звеньев; для соединения этих звеньев между собой и для присоединения группы к стойке или к подвижным звеньям механизма использовано 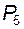 пар пятого класса; тогда для группы, согласно (1.1), можно записать
пар пятого класса; тогда для группы, согласно (1.1), можно записать
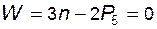 , (1.2)
, (1.2)
или
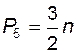 . (1.3)
. (1.3)
Из (1.3) заключаем, что группа может состоять только из четного числа звеньев, число пар пятого класса в группе всегда в полтора раза больше числа звеньев. Те пары, с помощью которых группа присоединяется к механизму, называют внешними, их количество определяет порядок группы; остальные пары, посредством которых звенья группы соединяются между собой, называют внутренними.
После отсоединения от механизма всех структурных групп останется стойка и начальные звенья в количестве W (речь идет о фактической степени подвижности механизма, рассчитанной после исключения пассивных связей и местных подвижностей). Каждое начальное звено со стойкой называют начальным механизмом; таким образом, механизм состоит из W начальных механизмов и некоторого количества структурных групп, присоединенных в строго определенном порядке, который отражают в специальной записи, называемой формулой строения. Например, механизм с двумя степенями свободы, содержащий шесть структурных групп, может иметь такое строение

| (1.4) |
В зависимости от количества звеньев в группе и способа их соединения между собой группы делят на классы.
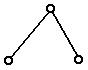
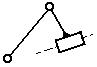
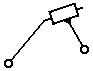
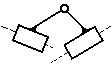
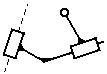
Все двузвенные группы ( 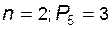 ) являются группами II класса второго порядка; дополнительно эти группы, в зависимости от количества поступательных пар, использованных при их формировании, делятся на виды (рис. 1.10).
) являются группами II класса второго порядка; дополнительно эти группы, в зависимости от количества поступательных пар, использованных при их формировании, делятся на виды (рис. 1.10).
| 
| 
| 
| 
|
| 1 вид | 2 вид | 3 вид | 4 вид | 5 вид |
| Рис. 1.10 Группы II класса |
Класс групп, состоящих более чем из двух
1. В основе любого механизма лежит один или несколько начальных механизмов. Начальный механизм – это начальное звено со стойкой.звеньев, определяется числом вершин (или сторон) многоугольника, образуемого внутренними кинематическими парами на структурной схеме группы, которая строится по следующим правилам:
· все вращательные и поступательные пары пятого класса изображают на этой схеме как вращательные;
· звенья, участвующие в нескольких кинематических парах, изображаются в виде соответствующих многоугольников.
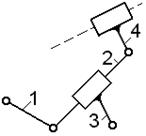
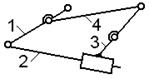
На рис. 1.11 и 1.12 для удобства сопоставления помещены рядом друг с другом кинематические и структурные схемы двух групп различных классов.
| 
| 
| 
|
| а) Кинематическая схема | б) Структурная схема | а) Кинематическая схема | б) Структурная Схема |
| Рис. 1.11 Группа III класса 3 порядка | Рис. 1.112 Группа IV класса 2 порядка |
На структурной схеме для большей наглядности можно те шарниры, которым на кинематической схеме соответствуют поступательные пары, помечать буквой «п».
В структурных схемах групп III класса внутренние шарниры образуют один или несколько треугольников жесткой (неизменяемой) конфигурации; в схемах групп более высоких классов встречаются многоугольники (изменяемой конфигурации) с четырьмя и большим числом сторон, которое и определяет класс группы.
Отметим, что классификации Л. В. Ассура подчиняются только те плоские механизмы, у которых начальные звенья образуют кинематические пары со стойкой.
1.6. Порядок структурного исследования плоского
механизма
1) Пронумеровать все звенья механизма (если номера звеньев не указаны); неподвижному звену (стойке) обычно присваивают последний номер.
2) Рассчитать степень подвижности механизма W и проанализировать полученный результат; при наличии местных подвижностей и (или) пассивных связей избавиться от них, и повторить расчет W – в результате должна получиться фактическая степень подвижности механизма.
3) Произвести замену всех высших кинематических пар фиктивными звеньями и низшими парами (замену следует производить непосредственно на кинематической схеме механизма, используя контактные нормали и центры кривизны профилей); подтвердить расчетом величину W – она должна остаться прежней.
Если кинематическая схема сложна для анализа, можно для облегчения изобразить структурную схему по описанным ранее правилам (при этом нумерация звеньев обязательно должны быть сохранена).
4) Выбрать начальные звенья механизма (если они не были заданы условием задачи): если после структурного исследования механизма будет выполняться его кинематический расчет, то начальные звенья совпадают с входными, т.е. с теми, которым заданы законы движения; при последующем силовом анализе механизма за начальные звенья принимают те, к которым приложены неизвестные внешние силы или вращающие моменты.
Написать формулу строения механизма по типу (1.4); каждому варианту выбора начальных звеньев соответствует единственный вариант этой формулы.
Вопросы для самопроверки
1. Дайте определения понятиям: механизм; звено; кинематическая пара; кинематическая цепь; кинематическое соединение.
2. Определите понятие «обобщенная координата механизма».
3. Что такое «степень подвижности механизма»? В каких случаях возникают местные подвижности и пассивные связи? Как влияет на степень подвижности механизма наличие в его схеме кратных шарниров?
4. Опишите цели замены высших кинематических пар низшими и порядок такой замены.
5. Что представляют собой структурная группа и начальный механизм?
6. По каким признакам устанавливают класс и порядок структурной группы?
7. Какие звенья выбирают в качестве начальных при кинематическом анализе механизма? То же – при силовом анализе?2. Сложный механизм получается путем наслоения групп Ассура.
Группа Ассура – это кинематическая цепь с нулевой степенью подвижности относительно тех звеньев, с которыми входят в кинематические пары свободные элементы ее звеньев, и не распадающаяся на более простые цепи, обладающие также нулевой степенью подвижности.
Классификация Ассура применима для плоских механизмов с парами V класса.
Структурные группы Ассура делятся на классы. Механизмы классифицируются по степени сложности групп входящих в их состав. Класс и порядок механизма определяется классом и порядком наиболее сложной из входящих в него групп. Особенность структурных групп Ассура - их статическая определимость. Если группу Ассура свободными элементами звеньев присоединить к стойке, то образуется статически определимая ферма. Используя группы Ассура удобно проводить структурный, кинематический и силовой анализ механизмов. Группы Асура делятся на классы. Группа, имеющая два звена и три пары V класса, называется группой II класса. Группы Ассура II класса делятся на пять видов:
8. Опишите последовательность структурного анализа плоского механизма.
Задачи
| II класс 1 вид | II класс 2 вид | II класс 3 вид | II класс 4 вид | II класс 5 вид |
Класс группы Ассура выше второго определяется видом замкнутой фигуры, образованной внутренними кинематическими парами. По числу внешних кинематических пар группы делятся на порядки.
Порядок структурного исследования.
1.Определяют степень свободы механизма.
2.1.Заменяют пары IV класса кинематическими цепями с парами V класса
3.1.Для сложных схем рисуют структурную схему, при этом поступательные пары заменяют на вращательные, звенья входящие в три кинематические пары рисуют в виде треугольников, в четыре – четырехугольников. Нумерация звеньев сохраняется.
4.1.Записывают формулу строения механизма (структурная формула), при этом число начальных механизмов равно числу степеней свободы механизма.
1.
Задача 1.01
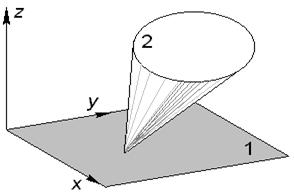 
| Задача 1.01 Установить класс кинематической пары, образуемой плоской (1) и конической (2) поверхностями (конус касается плоскости только вершиной). По отношению к координатным осям xyz перечислить все виды допускаемых движений конуса относительно плоскости. | ||||||
| Задача 1.02 Для плоской кинематической пары, представленной на рисунке, установить: - высшая пара, или низшая; - класс кинематической пары; - число подвижностей в относительном движении звеньев 1 и 2. |
| ||||||
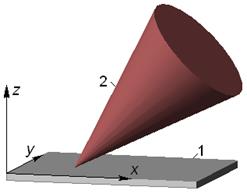
Задача 1.03
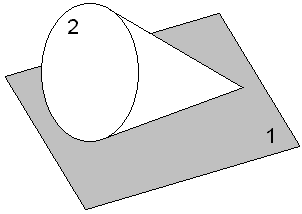 
| Конус 2 касается плоскости 1 своей образующей. Для кинематической пары, образуемой указанными звеньями, установить класс и число подвижностей в относительном движении звеньев 1 и 2 (назвать эти подвижности по отношению к какой-либо системе координат, связанной с плоскостью). | ||||||
Задача 1.04
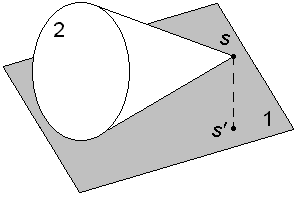 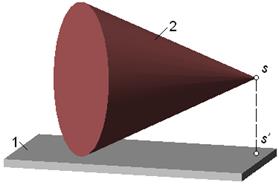
|
Конус 2 касается плоскости 1 кромкой своего основания, вершина конуса s удалена от плоскости на расстояние 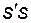 s, где s, где 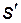 – проекция вершины конуса на плоскость.
Для кинематической пары, образуемой указанными звеньями, установить класс и число подвижностей в относительном движении звеньев 1 и 2 (назвать эти подвижности по отношению к какой-либо системе координат, связанной с плоскостью). – проекция вершины конуса на плоскость.
Для кинематической пары, образуемой указанными звеньями, установить класс и число подвижностей в относительном движении звеньев 1 и 2 (назвать эти подвижности по отношению к какой-либо системе координат, связанной с плоскостью).
| ||||||
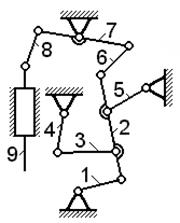
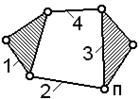
| Задача 1.05 Для механизма с одной степенью свободы указать номера звеньев, образующих группу III класса 3-го порядка при начальном звене 9. | ||||||
| Задача 1.06(см. рисунок к задаче 1.05) Для механизма с одной степенью свободы указать номера звеньев, образующих группу III класса 3-го порядка при начальном звене 4. | |||||||
| Задача 1.07(см. рисунок к задаче 1.05) Для механизма с одной степенью свободы написать формулу строения механизма при начальном звене 5. | |||||||
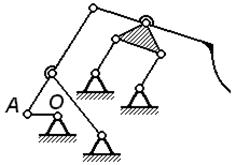
| Задача 1.08 Для механизма с одной степенью свободы пронумеровать звенья и написать формулу строения механизма при начальном звене OA. | ||||||
| Задача 1.09 Считая звено 1 начальным, указать структурную группу, которую можно отсоединить от механизма, не нарушая его подвижности (ответ обосновать). | 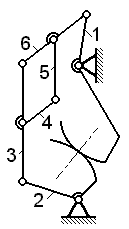
| ||||||
| Задача 1.10(см. рисунок к задаче 1.09) Считая звено 2 начальным, указать структурную группу, которую можно отсоединить от механизма, не нарушая его подвижности (ответ обосновать). | |||||||
| Задача 1.11 Для механизма с одной степенью свободы указать номера звеньев, образующих группу III класса 3-го порядка при начальном звене 9. | 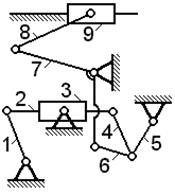
| |
| Задача 1.12(см. рисунок к задаче 1.11) Для механизма с одной степенью свободы указать номера звеньев, образующих группу III класса 3-го порядка при начальном звене 5. | ||
| Задача 1.13(см. рисунок к задаче 1.11) Считая звено 9 начальным, указать структурную группу, которую можно отсоединить от механизма, не нарушая его подвижности (ответ обосновать). | ||
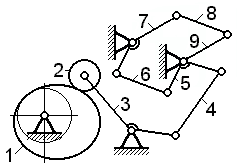
| Задача 1.14 Считая звено 1 начальным, указать две первые структурные группы, которые можно поочередно отсоединить от механизма, не нарушая его подвижности (ответ обосновать). | |
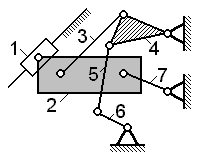
| Задача 1.15 Для механизма с одной степенью свободы указать номера звеньев, образующих группу III класса 3-го порядка при начальном звене 4. | |
| Задача 1.16(см. рисунок к задаче 1.15) Для механизма с одной степенью свободы указать номера звеньев, образующих группу III класса 3-го порядка при начальном звене 6. | ||
| Задача 1.17(см. рисунок к задаче 1.15) Считая звено 1 начальным, указать структурную группу, которую можно отсоединить от механизма, не нарушая его подвижности (ответ обосновать). | ||
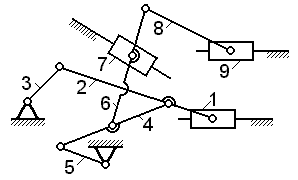 Задача 1.18
Считая звено 1 начальным, указать две первые структурные группы, которые можно поочередно отсоединить от механизма, не нарушая его подвижности (ответ обосновать). Задача 1.18
Считая звено 1 начальным, указать две первые структурные группы, которые можно поочередно отсоединить от механизма, не нарушая его подвижности (ответ обосновать).
| ||
| Задача 1.19(см. рисунок к задаче 1.18) Считая звено 5 начальным, указать две первые структурные группы, которые можно поочередно отсоединить от механизма, не нарушая его подвижности (ответ обосновать). | ||
| Задача 1.20(см. рисунок к задаче 1.18) Считая звено 3 начальным, указать две первые структурные группы, которые можно поочередно отсоединить от механизма, не нарушая его подвижности (ответ обосновать). | ||
| Задача 1.21(см. рисунок к задаче 1.18) Считая звено 5 начальным, указать номера звеньев, образующих группу III класса 3-го порядка. | ||
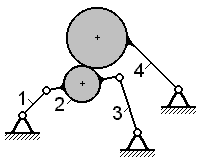
| Задачи 1.22 – 1.24 Для механизма с высшей кинематической парой построить заменяющий механизм; замену высшей пары произвести непосредственно на кинематической схеме. Написать формулу строения заменяющего механизма при начальном звене 4. | ||
К задаче 1.22
| К задаче 1.23

| К задаче 1.24

|
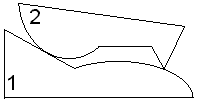
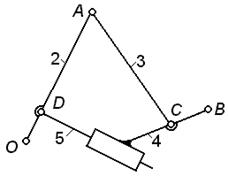
| Задачи 1.25 – 1.30 Если изображенная кинематическая цепь является структурной группой, указать ее класс и порядок (в противном случае объяснить, почему цепь не является группой). | ||||
К задаче 1.25
| К задаче 1.26

| К задаче 1.27
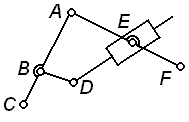
| ||
К задаче 1.28
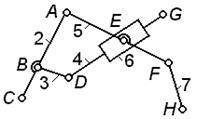
| К задаче 1.29
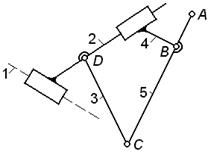 Направляющая 1 в состав
кинематической цепи не входит
Направляющая 1 в состав
кинематической цепи не входит
| К задаче 1.30
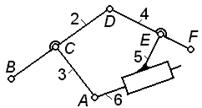
| ||
Дата добавления: 2021-12-14; просмотров: 629;











