Кинематика замкнутых механизмов
|
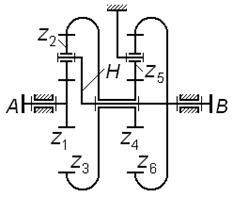
| Рис. 3.11 |
Проанализируем структуру комбинированного механизма, представленного на рис. 3.11; он включает в себя: дифференциальную ступень ( 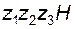 ) и рядовую кинематическую цепь (
) и рядовую кинематическую цепь ( 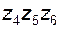 ).
).
Кинематика дифференциальной ступени описывается формулой Р. Виллиса
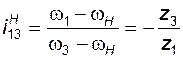 ; (3.23)
; (3.23)
если бы любые две из трех угловых скоростей 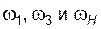 у этой ступени могли быть независимыми, то данный механизм имел бы две степени свободы. Однако, поскольку
у этой ступени могли быть независимыми, то данный механизм имел бы две степени свободы. Однако, поскольку 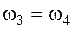 и
и 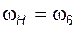 , то угловые скорости
, то угловые скорости 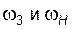 дифференциала связаны между собой соотношением
дифференциала связаны между собой соотношением
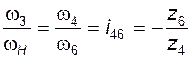 . (3.24)
. (3.24)
Таким образом, звенья 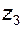 и H дифференциала имеют жесткую кинематическую связь в виде рядовой цепи (
и H дифференциала имеют жесткую кинематическую связь в виде рядовой цепи ( 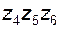 ); эта цепь как бы замыкает дифференциальную ступень, и механизмы такого типа обычно называют замкнутыми дифференциалами.
); эта цепь как бы замыкает дифференциальную ступень, и механизмы такого типа обычно называют замкнутыми дифференциалами.
Если учесть соотношения 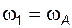 и
и 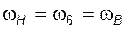 , то (3.23) можно записать в виде
, то (3.23) можно записать в виде
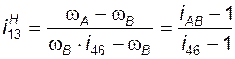 ; (3.25)
; (3.25)
тогда передаточное отношение механизма
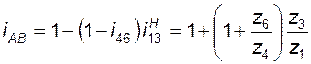 . (3.26)
. (3.26)
Таким образом, для анализа кинематики подобных механизмов можно придерживаться следующей методики:
1) выделить в схеме дифференциальную ступень, содержащую водило, размещенные на нем сателлиты и центральные колеса, зацепляющиеся с этими сателлитами; для выделенной ступени написать формулу Р. Виллиса по типу (3.23), ни одна из угловых скоростей не должна быть равна нулю (т.е. ступень не должна содержать неподвижных колес);
2) выделить в схеме замыкающую кинематическую цепь, связывающую между собой какие-то центральные звенья дифференциальной ступени; если эта цепь рядовая, то написать для нее формулу по типу (3.24);
3) написать уравнения внутренних кинематических связей (для данного механизма – формулы 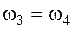 и
и 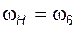 );
);
4) написать уравнения внешних кинематических связей (для данного механизма – формулы 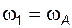 и
и 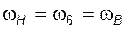 );
);
5) используя зависимости, полученные в пунктах 2 – 4, выразить каждую угловую скорость, входящую в формулу Р. Виллиса (п. 1) через 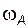 или
или 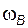 , чтобы получить уравнение по типу (3.25); из этого уравнения вывести формулу для
, чтобы получить уравнение по типу (3.25); из этого уравнения вывести формулу для 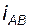 .
.
Дата добавления: 2021-12-14; просмотров: 445;











