Задачи, решаемые с помощью диаграмм динамической остойчивости

С помощью диаграммы динамической остойчивости можно решить те же задачи, что и с помощью диаграммы статической остойчивости. Особенно удобно решать задачи об определении динамического угла крена θ_дин и предельного дина-мического момента М_пр.дин . Например, если кренящий момент не зависит от θ, работа кренящего момента будет равна,

, (3.54) т.е. Т_кр - линейная функция от θ. Кстати, если θ =1 радиан, Т_кр = М_кр, что можно использовать для построения графика Т_кр(θ) (рис. 3.31). Работа восстанавливаю-щего момента равна

.

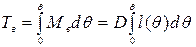Динамический угол крена определится в точке пересечения T_кр и Т_в.

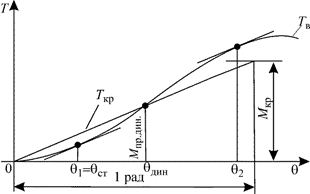
Рис. 3.31. Определение θ_дин и θ_ст на диаграмме динамической остойчивости

Статические углы крена определятся из равенства моментов, т.е.

.

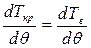Следовательно, необходимо провести касательные к кривой Т_в параллельно прямой Т_кр . В точках касания будет θ₁ = θ_ст и θ₂.

Предельный динамический момент М_пр.дин можно определить, проведя каса-тельную к кривой Т_в из начала координат и измерив ординату на расстоянии 1 радиан от начала координат (рис. 3.32), а предельный статический момент - проведя касательную к кривой Т_в в точке перегиба А, соответствующей максимуму диаграммы статической остойчивости, и измерив на расстоянии 1 радиан ординату ВС, отсчитываемую от прямой АВ, параллельной оси абсцисс.

С помощью диаграммы динамической остойчивости можно также решать задачи определения предельных статических и динамических моментов при действии различных комбинаций статически и динамически приложенных кренящих моментов.

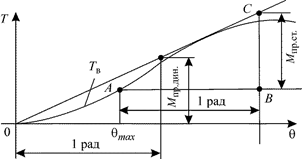
Рис. 3.32. Определение М_пр.ст и М_пр.дин с помощью диаграммы динамической остойчивости (переделать рисунок)

1. Судно плавает с начальным углом крена θ₀ от кренящего момента М₀ , обусловленного перемещением груза (такой момент будет статически приложенным; будем его считать постоянным). Подействовал динами-чески приложенный момент М₁, например, шквал. Необходимо определить предельный динамический момент.

Вначале определяется угол θ₀ для заданного статически приложенного момента М₀, как это было показано выше (см. рис. 3.31).

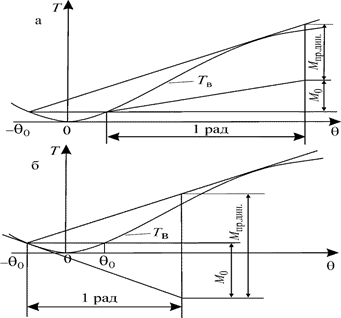
Рис 3.33. Определение предельного динамического момента по диаграмме динамической остойчивости при действии груза и шквала

Дальнейшее решение иллюстрируется рис. 3.33. Из точки на диаграмме динамической остойчивости, соответствующей углу θ₀ , проводится касательная к диаграмме и на расстоянии 1 радиан восстанавливается перпендикуляр до пересечения с касательной. Отложив от основания перпендикуляра М₀, получим отрезок до вершины треугольника, который и будет равен М_пр.дин. В случае а, когда момент М₁ действует на встречный наклонный борт, М₀ откладывается вниз (наружу от треугольника), а в случае б – вверх (внутрь треугольника). Видно, что при в случае а М_пр.дин будет гораздо больше, чем в случае б.

2. Судно плавает с начальным углом крена θ₀ от кренящего момента М₀ , обусловленного постоянно дующим ветром. Подействовал динамически приложенный момент М₁. Необходимо определить предельный динамический момент.

Если динамически приложенный момент М₁ не является моментом от шквала, задача решается совершенно также, как и предыдущая. Однако, если налетает шквал, решение будет качественно иным.

Если вспомнить объяснения решения этой задачи по диаграмме статической остойчивости, то при действии шквала из-за снятия ветра судно как - бы переходит на противоположный борт, а затем для него определяется предельный момент (см. предыдущую задачу). Но можно решение получить проще, проводя касательную к диаграмме динамической остойчивости прямо из точки, соответствующей углу θ_о, восстановив на расстоянии 1 радиана перпендикуляр и измерив расстояние от основания перпендикуляра до точки пересечения его с касательной (рис. 3.34). В случае а (при действии шквала на наветренный борт) предельный момент будет гораздо меньше, чем при действии на подветренный.

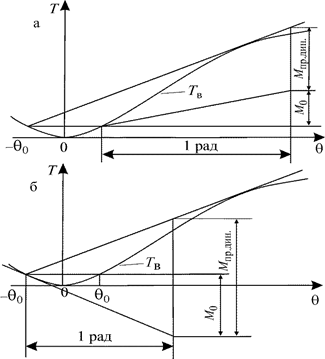
Рис. 3.34. Определение предельного динамического момента по диаграмме динамической остойчивости при действии ветра и шквала

3. Судно качается на взволнованном море с амплитудой качки θ_r , т.е. испытывает воздействие возмущающего момента от волн. Подействовал шквал или динамически приложенный момент другой физической природы. Необходимо определить предельный динамический момент.

С помощью диаграммы статической остойчивости эта задача решалась также, как и при действии постоянно дующего ветра и шквала, только вместо начального угла крена θ₀ использовалась амплитуда качки θ_r. При решении задачи с помощью диаграммы динамической остойчивости мы будем использовать тот же подход, что и в предыдущем случае (рис. 3.35), восстановив аналог М₀ с помощью касательных при углах θ_r (нижние треугольники).

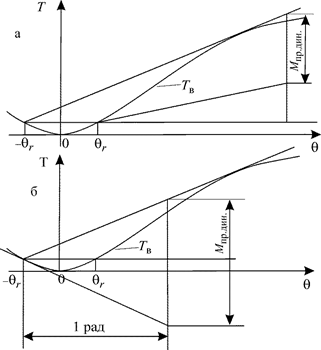
Рис. 3.35. Определение предельного динамического момента по диаграмме динамической остойчивости при качке и действии шквала (подправить случай а)

Необходимо отметить, что решение задач с помощью диаграмм статической и динамической остойчивости не является самоцелью, а используется на практике для обеспечения безопасности плавания судов, особенно для решения проблем нормирования остойчивости при эксплуатации судов на взволнованном море при одновременном действии ветра (постоянно дующего и порывистого) и волн. Об этом рассказывается в дальнейшем.

Решение с помощью диаграмм статической остойчивости обычно нагляднее и точнее, поэтому в последнее время при нормировании остойчивости судов ими пользуются более широко.