Изменение посадки и остойчивости судна при переносе, приеме и расхо-довании груза. Понятие о нейтральной плоскости. Метацентрическая диа-грамма

Перенос, прием и расходование грузов являются повседневными операциями в процессе эксплуатации судна. Такие операции приводят к изменению посадки (средней осадки, углов крена и дифферента) и остойчивости судна. Как правило, это изменение с достаточной для практики точностью можно оценить по формулам начальной остойчивости. Пересчет диаграмм статической и динамической остойчивости проводят лишь в случаях, связанных главным образом с обеспечением безопасности плавания.

Перенос груза

Пусть на судне некоторый груз p массой m перенесен так, что ЦТ этого груза переместился из точки с координатами x₀, y_­0, z₀ в точку с координатами x₁, y_­1, z₁. Тогда масса всего судна не изменится, но изменится положение его ЦТ. Раскладывая фактическое перемещение ЦТ груза на три взаимно перпен-дикулярных перемещения, параллельные координатным осям, рассматриваем продольное перемещение l_x = x₁— x₀, поперечное перемещение l_у = y₁ — y₀ и вертикальное перемещение l_z = z₁ — z₀ (рис. 2.14).

Исследование одновременного воздействия всех трех перемещений на посадку и остойчивость судна приводит к сложным выкладкам, поэтому вначале разберем перенос груза по вертикали на расстояние l_z, а затем перенос груза в горизонтальной плоскости на расстояния l_у и l_х.

Перенос груза по вертикали. Перемещение ЦТ судна можно найти с помощью теоремы теоретической механики о статических моментах, согласно которой

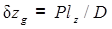. (2.28)

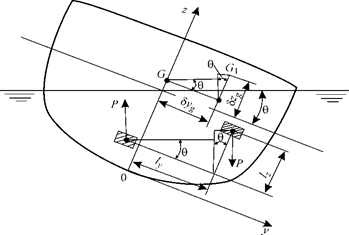
Рис. 2.14. Наклонение судна при переносе малого груза в поперечной плоскости

Согласно (2.17) и (2.21) метацентрические высоты равны

;

.

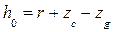Для приращений метацентрических высот по аналогии можно записать

;

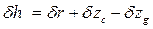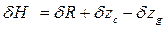. (2.29)

Однако при вертикальном переносе груза изменения водоизмещения, осадки и формы подводной части судна нет, поэтому первые два слагаемых в каждой из формул (2.29) равны нулю. Таким образом, изменения метацентрических высот будут одинаковы

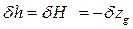. (2.30)

Подставляя в эту формулу выражение (2.28), получим

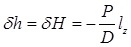, (2.31)

Если груз переносится вниз, то 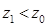, 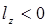и согласно формуле (2.31) 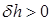, т. е. начальная остойчивость увеличивается.

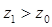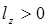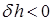Если же груз переносят вверх, то , и , т. е. начальная остойчивость снижается. Очевидно, возможен случай, когда при переносе грузов вверх поперечная метацентрическая высота станет равной нулю или даже отрицательной. На практике таких случаев следует избегать, поскольку они запрещены правилами безопасной эксплуатации судов.

Для большинства судов продольная метацентрическая высота намного больше поперечной. Поэтому в практических расчетах поправкой 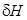почти всегда можно пренебречь по сравнению с .

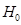Таким образом, новые метацентрические высоты будут равны

;

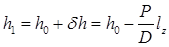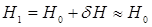. (2.32)

Восстанавливающие моменты будут соответственно равны

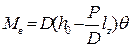; (2.33)

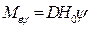. (2.34)

Перенос груза по горизонтали. При переносе груза по оси Оу на расстояние l_у возникает кренящий момент 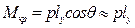. Статическое равновесие наступает при равенстве кренящего и восстанавливающего моментов 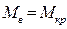, или с учетом (2.33)

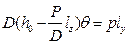. (2.35)

Из этой формулы можно получить угол крена, с которым будет плавать судно

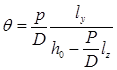. (2.36)

В случае переноса груза на правый борт 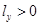и 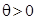, а в случае переноса на левы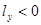й и .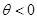

При переносе груза по оси Ох возникает дифферентующий момент 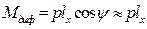и все рассуждения относительно равенства дифферентующего и восстанавливающего моментов можно повторить. Окончательно получим угол дифферента

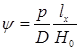. (2.37)

Если груз переносится в нос, то 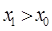, , 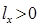а значит и 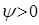, т. е. судно получает дифферент на нос. Если же груз переносится в корму, то 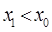, , 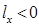, 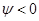т. е. судно дифферентуется на корму. Изменение осадок носом и кормой можно определить, используя теорему Эйлера. Проведем через точку F — ЦТ площади ватерлинии В₀Л₀ судна в прямом положении — наклонную ватерлинию В 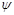Л 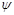под углом дифферента 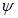(рис. 2.15). Тогда для изменения осадок носом 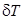и кормой 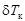можно записать:

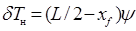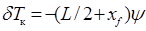; , (2.38)

где положительные значения 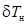и 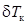соответствуют увеличению осадок носом T_н и кормой T_к, а отрицательные – их уменьшению. Дифферент (в метрах) определяется выражением:

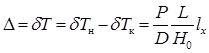. (2.39)

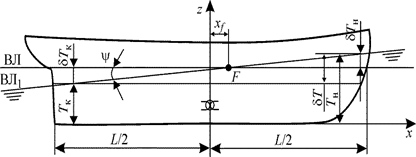
Рис. 2.15. Определение осадок носом и кормой при приеме малого груза

Если 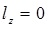, т.е. груз переносится только по горизонтали

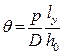; (2.36^’)

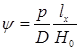. (2.37)