Некоторые задачи плавучести, решаемые в процессе эксплуатации судна

В процессе эксплуатации на судне расходуются грузы (вода, топливо и т. д.) или, наоборот, принимаются грузы. Кроме того, судно эксплуатируется в морях с водой различной плотности, зависящей от солености и температуры. При этом будет наблюдаться изменение осадки и координат ЦТи ЦВ. Контроль за ними является обязательным, поскольку от знания их зависит безопасность судна.

1.14.1. Изменение осадки и координат ЦТ и ЦВпри приеме и расходовании малого груза. Кривая числа тонн на 1 см осадки

Груз называется малым, если при его приеме или расходовании судно в пределах изменения осадки можно считать прямобортным. На практике считается, что условие прямобортности для судов обычных архитектурных типов выполняется, если масса груза не превосходит 10 % массы судна.

При приеме малого груза весом p = mg (рис. 1.35) осадка судна
должна измениться таким образом, чтобы дополнительная сила поддержания ρgδV компенсировала силу тяжести груза p, т.е. должно выполняться равенство mg = ρgδV , или m = ρδV.

Поскольку груз мал, можно в пределах изменения осадки считать борта судна вертикальными и выразить δV через приращение осадки и площадь ватерлинии

δV =SδT , (1.91)

тогда

p = ρgSδT . (1.92)
Отсюда изменение осадки

δT = p/(ρgS). (1.93)

С помощью формулы (1.93) и с учетом того, что p = mg, можно рассчитать и построить кривую числа тонн на 1 см осадки. Если положить δT = 1 см = = 0,01 м, а m = q, получим

q = ρS/100 - (1.94)
число тонн на 1 см осадки. Таким образом, достаточно изменить лишь масштаб на оси ординат строевой по ватерлиниям, чтобы найти зависимость q от z. С помощью q легко найти значение δT (в сантиметрах) при приеме груза по формуле

δT = m/q. (1.95)

В проектной документации обычно рядом с грузовой шкалой изобра-
жают шкалу числа тонн на 1 см осадки (см. рис. 1.16).

При приеме груза кроме осадки будут меняться также координаты
ЦТ и ЦВ судна.

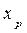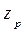Обозначив координаты центра тяжести груза , и (рис.1.35) и составив уравнения статических моментов масс относительно координатных
плоскостей, получим

;

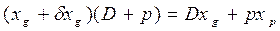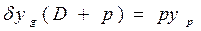; (1.96)

,

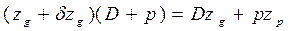где 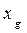, 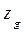— координаты ЦТ судна до приема груза. При написании второго уравнения учтено, что для судна в прямом положении 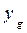=0.

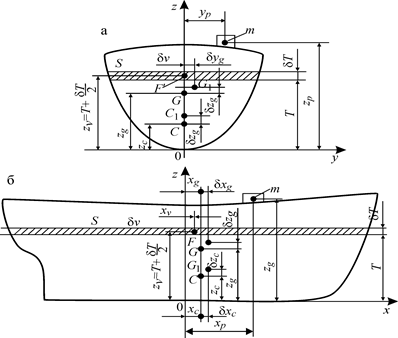
Рис.1.35. К определению изменения осадки и приращений координат ЦТ и ЦВ при приеме малого груза: а — поперечный; б — продольный разрез судна

Из системы уравнений (1.96) легко определить изменения координат ЦТ судна:

;

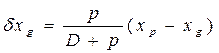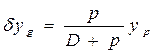; (1.97)

.

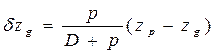В соответствии с (1.97) получается, что изменения координат ЦТне будет, если груз принят в ЦТ судна.

Изменение координатЦВ можно определить из уравнений статических моментов объемов относительно координатных плоскостей:

;

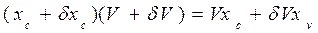; (1.98)

.

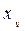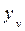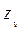Здесь , и — координаты ЦТдополнительного объема δV.

Из рис. 1.35 следует, что при приеме малого груза 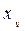= 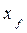; 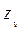= Т + δT / 2 , a 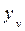= 0, так как судно остается по-прежнему симметричным относительно ДП.

Подставив эти величины в уравнения (1.98), можем вычислить

;

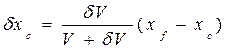; (1.99)

.

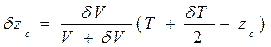Умножив числители и знаменатели уравнений (1.99) на ρg, получим

;

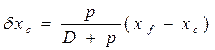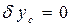; (1.100)

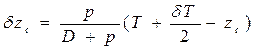
Системы (1.97) и (1.100) верны и для случая снятия груза, но только
вместо p надо в них подставлять - p.

Формулы (1.97) и (1.100) используют в дальнейшем при расчетах остойчивости.

Чтобы судно не получило при приеме или снятии груза ни крена, ни дифферента, необходимо выполнять условия δx_g = δх_с и δy_g = δу_с ,или в развернутом виде на основании выражений (1.97) и (1.100)

;

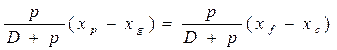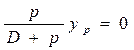(1.101) (1.101

С учетом того, что х_g = х_с (из второго условия плавучести), окончательно имеем

х_р = х_f, ; у_f = 0 . (1.102)

Таким образом, чтобы судно при приеме или расходовании груза не получило ни крена, ни дифферента, центр тяжести этого груза должен находиться на одной вертикали с центром тяжести площади ватерлинии.

Определение углов крена и дифферента в случае приема груза в произвольную точку связано с достаточно сложными расчетами и выполняется в дальнейшем.