Определение кинематических передаточных функций кулачкового механизма

Связь между кинематическими параметрами толкателя - ускорением 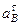, скоростью 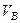и перемещением 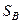определяется известными соотношениями:

,

,

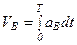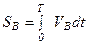где Т - время одного оборота кулачка.

Так как закон изменения скорости кулачка неизвестен, приведенные зависимости нельзя использовать непосредственно, но их можно выразить через кинематические передаточные функции, которые не зависят от времени:

,

.

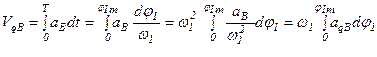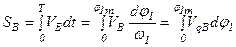При расчете размеров и координат профиля кулачка кулачкового механизма определяющими являются ход толкателя, угол рабочего профиля кулачка и функциональная зависимость ускорения (относительного ускорения) толкателя от угла поворота кулачка. Если задать эту зависимость в аналитической форме, то последующим интегрированием могут быть получены зависимости кинематической передаточной функции скорости и перемещения толкателя.

Любую непрерывную дифференцируемую функцию вида 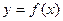можно представить разложением в ряд:

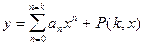, (7.1)

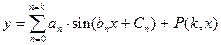. (7.2)

(7.1) - полиномиальное разложение;

(7.2) - разложение в тригонометрический ряд;

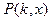- остаточный член.

Двойное интегрирование выражений (1) и (2) позволяет получить:

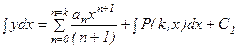, (7.3)

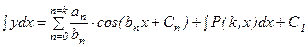, (7.4)

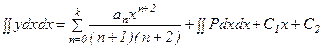, (7.5)

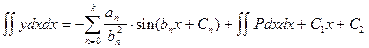, (7.6)

где С₁ , С₂ - константы интегрирования.

Если предположить что 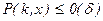, то интегралы от Р из формул (7.3)-(7.6) можно исключить. Таким образом, имея зависимости 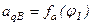вида (7.1) или (7.2), легко получить аналитические зависимости 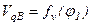вида (7.3) или (7.4) и зависимости 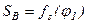вида (7.5) или (7.6).

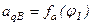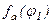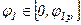При расчетах кулачкового механизма с поворотным толкателем реализован алгоритм, вычисляющий значения первого и второго интеграла относительного ускорения толкателя для определения углов поворота кулачка. Следует заметить, что в общем виде может иметь точки разрыва. При этом функция при разбивается на участки:

,

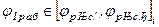где 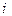- индекс участка (режима).

Так что функция 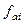- кусочно-непрерывная дифференцируемая функция в области своего определения 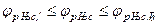, каждый i-й участок называется режимом, при этом:

.

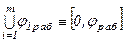Чтобы избежать неопределенности в задании функции 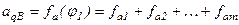, отрезки 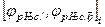открыты справа. Для обеспечения задания функции на 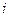- ом режиме 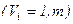предполагается, что 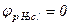. Требование 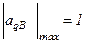не является обязательным.

Точность интегрирования определяется не шагом по углу поворота, а точностью задания функции на участке, т.е. величиной .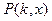

Если исходная функция заданна в виде графика или таблицы значений, то решение получают при помощи численных или графических методов. Для определения передаточной функции скорости толкателя интегрируют заданную функцию ускорения толкателя, интегрируя полученную функцию скорости, находят функцию перемещения толкателя. Обычно применяется численное интегрирование методом трапеций по формулам:

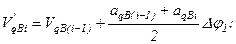
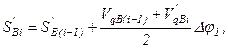
где - 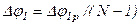приращение угла поворота кулачка на шаге интегрирования,

N - число равноотстоящих точек, в которых заданны значения переменной.

Примечание:

В течение цикла движения толкатель кулачкового механизма должен переместиться из начального положения на величину хода h , а затем возвратиться в исходное положение, то есть перемещение толкателя на фазе удаления равно перемещению на фазе сближения. Следовательно, график кинематической передаточной функции скорости должен удовлетворять условию:

,

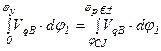где j_со - угловая координата начальной точки фазы сближения.

Скорость и кинематическая передаточная функция скорости толкателя на фазах ближнего и дальнего выстоя равны нулю. Чтобы эти условия выполнялись необходимо выполнить соотношения:

,

,

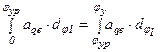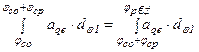где j_yp - угловое перемещение при разгоне на фазе удаления;

j_ср - угловое перемещение при разгоне на фазе сближения;

j_ст = j_раб - (j_со + j_ср) - угловое перемещение при торможении на фазе сближения.

Эти условия необходимо учитывать при построении безразмерных графиков передаточной функции скорости и передаточной функции ускорения, выравнивая соответствующие указанным интегралам площади над осью абсцисс и под ней.

При работе над листом проекта с использованием графического интегрирования (рис. 7.3) все три графика располагают один под другим на одинаковой базе по оси абсцисс, которую удобно выбирать в пределах 150...240 мм. График скорости 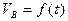толкателя (рис. 7.3 б) получается (строится) методом графического интегрирования из графика ускорения толкателя. Для этого на продолжении оси t графика ускорений с левой стороны выбирается отрезок интегрирования К₁ = 30...50 мм. После построения графика скорости строится график перемещений толкателя рис. 3в. Для этого также на продолжении оси абсцисс t графика 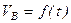откладывается отрезок интегрирования К₂. Можно принимать К₁ = К₂. Или принять их равными m_j. В зависимости от принятых отрезков интегрирования на графике 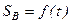ордината 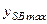получается больше или меньше. Если частота вращения кулачка n₁ (с^-1) и максимальное перемещение (ход) толкателя h в исходных данных на проект заданы, то можно определить следующие масштабы:

Масштаб времени, мм/с:

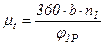, (7.7)

Масштаб перемещений, мм/м:

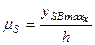, (7.8)

Масштаб скорости, мм / мс^-1:

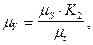(7.9)

Масштаб ускорений, мм / мс^-2:

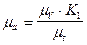(7.10)

где 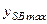- максимальная ордината с графика перемещений точки В центра ролика толкателя, мм;

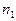- частота вращения кулачка, c^-1.

Если в задании на проект значение угловой скорости или частоты вращения кулачка не заданы, то можно интегрировать заданный график по углу поворота кулачка 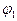и получить графики кинематических передаточных функций. Для перехода от вычисленных интегралов 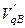и 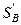к действительным значениям кинематической передаточной функции скорости 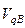и перемещения 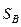определяются масштабы, которые вычисляются с учетом заданного максимального перемещения (хода) толкателя h и максимального вычисленного перемещения 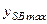из массива перемещений .

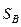Масштаб угла поворота, мм/рад:

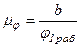, (7.11)

Масштаб передаточной функции скорости ,мм/м рад^-1 :

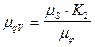, (7.12)

Масштаб передаточной функции ускорения, мм/м рад^-2 :

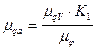, (7.13)

где 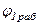- угол рабочего профиля кулачка в радианах,

К₁ ,К₂ - отрезки интегрирования, мм.

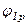- угол рабочего профиля кулачка в градусах;

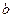- база графика, мм;

В массиве 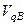отыскиваются максимальное 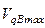и минимальное 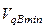значения и соответствующие им углы 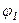и перемещения толкателя .

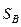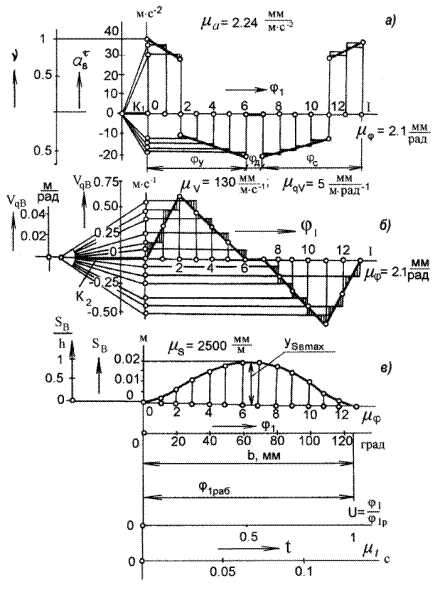
Рис. 7.3. Аналоги ускорений, скоростей и перемещений

кулачка