Построение профиля кулачка

Принимаем масштаб построения тот же, что и при определении r_min.

Минимальный радиус теоретического профиля кулачка ρ_min получаем равным r_min :

r_min = ρ_min = 8,6 мм

Исходя из условия R_ролика ≤ ρ_min принимаем R_ролика = 0,6 ρ_min = 5,5 мм.

Действительный профиль кулачка строим на сгибе дуг радиуса ролика.

Углы давления

Теоретическое значение угла давления получим из построения по определению r_min кулачка_. Соединяем центры вращения кулачка O с точками H_i, измеряем углы α_i между линиями OH_i и вертикально параллельной вектору скорости движения толкателя. Результаты заносим в таблицу 5.2

Таблица 5.2

Фактические углы давления применяем на кулачке в точках 1 и 11, где они достигают максимума. Углы заключены между нормалью к профилю кулачка и линии толкателя. Замеры показывают, что эти углы α₁° и α₁₁° совпадают с α_доп°.

α_доп = 90°- γ_min = 90° - 60° = 30°

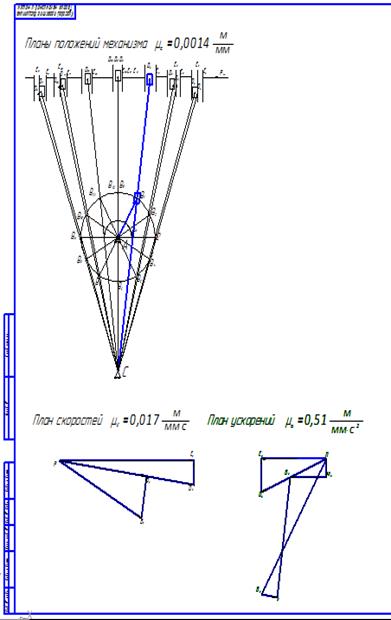
Рис. 5.1. Кинематический анализ

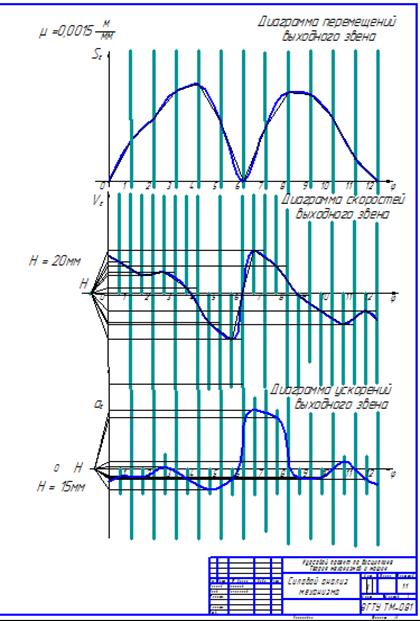
Рис. 5.1. Продолжение

Рис. 5.2. Силовой анализ

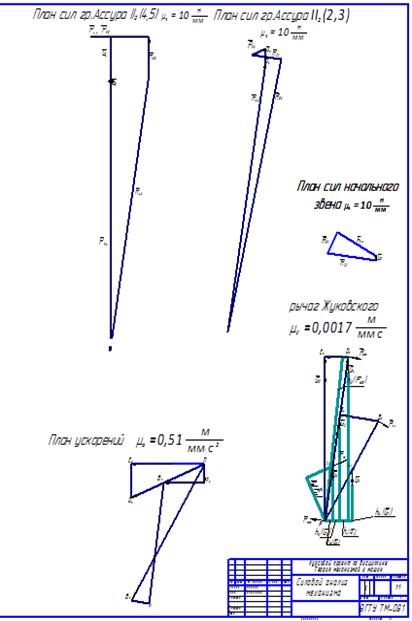
Рис. 5.2. Продолжение

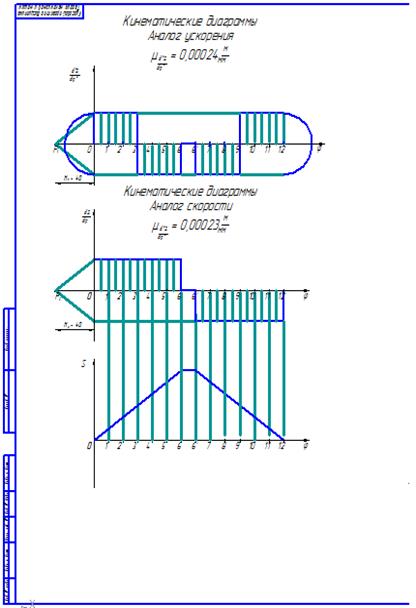
Рис. 5.3. Синтез кулачкового механизма

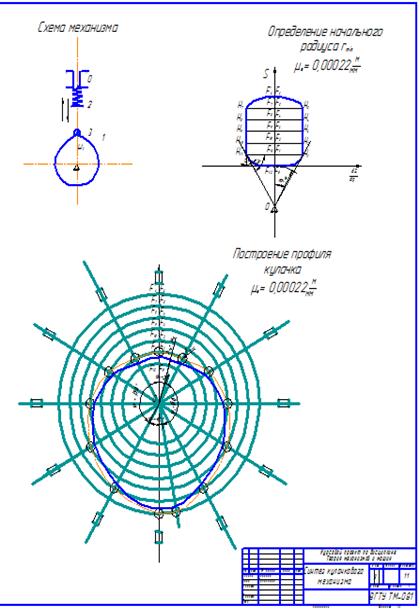
Рис. 5.3. Продолжение
6. ОСНОВЫ ТЕОРИИ ЗУБЧАТОГО ЗАЦЕПЛЕНИЯ

Профили зубьев пары колес должны быть сопряженными, т. е. заданному профилю зуба одного колеса должен соответствовать вполне определенный профиль зуба другого колеса. Чтобы обеспечить постоянство передаточного числа, профили зубьев нужно очертить такими кривыми, которые удовлетворяли бы требованиям основной теоремы зацепления.
Основная теорема зацепления. Для доказательства теоремы рассмотрим пару сопряженных зубьев в зацеплении (рис. 6.1). Профили зубьев шестерни и колеса касаются в точке S, называемой точкой зацепления. Центры вращения О₁ и О₂ расположены на неизменном расстоянии a_w друг от друга.

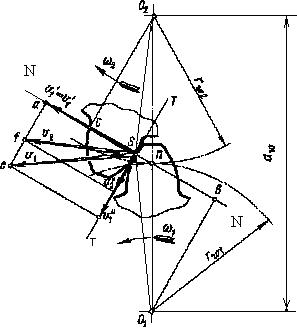
Рис. 6.1 схема зацепления пары зубчатых колес

Зуб шестерни, вращаясь с угловой скоростью w₁, оказывает силовое действие на зуб колеса, сообщая последнему угловую скорость w₂. Проведем через точку S общую для обоих профилей касательную ТТ и нормаль NN. Окружные скорости точки S относительно центров вращения О₁ и О₂:

v₁ = O₁ Sw₁ и v₂ = O₂ Sw₂

Разложим v₁ и v₂ на составляющие v'₁ и v'₂ по направлению нормали NN и составляющие v''₁ и v''₂ по направлению касательной ТТ. Для обеспечения постоянного касания профилей необходимо соблюдение условия v'₁ = v'₂, в противном случае при v'₁ < v'₂ зуб шестерни отстанет от зуба колеса, а при v'₁ > v'₂ произойдет врезание зубьев. Опустим из центров O₁ и О₂ перпендикуляры O₁B и О₂С на нормаль NN.
Из подобия треугольников aeS и BSO₁ :

v'₁ / v₂ = O₁B / O₁S,

откуда:

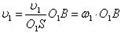
Из подобия треугольников afS и CSO₂ v'₂ / v₂ = O₂C / O₂S, откуда v'₂ = (v₂/O₂S) O₂C = w₂ *O₂C. Ho v'₁ = v'₂, следовательно, w₁ * O₁B = w₂ * O₂C. Передаточное число:

u = w₁ / w₂ = O₂C / O₁B. (6.1)

Нормаль NN пересекает линию центров О₁О₂ в точке П, называемой полюсом зацепления. Из подобия треугольников О₂ПС и О₁ПВ:

O₂C / O₁B = O₂П / O₁П = r_w1 / r_w2 (6.2)

Сравнивая отношения (6.1) и (6.2), получаем:

u = w₁ / w₂ = r_w1 / r_w2 = const (6.3)

Таким образом, основная теорема зацепления формулируется: для обеспечения постоянного передаточного числа зубчатых колес профили их зубьев должны очерчиваться по кривым, у которых общая нормаль NN, проведенная через точку касания профилей, делит расстояние между центрами O₁O₂ на части, обратно пропорциональные угловым скоростям.

Полюс зацепления П сохраняет неизменное положение на линии центров O₁O₂, следовательно, радиусы r_w1 и r_w2 также неизменны.

Окружности радиусов r_w1 и r_w2 называют начальными. При вращении зубчатых колес начальные окружности перекатываются друг по другу без скольжения, о чем свидетельствует равенство их окружных скоростей w₁r_w1 = w₂r_w2, полученное из формулы (6.3).

Из множества кривых, удовлетворяющих требованиям основной теоремы зацепления, практическое применение в современном машиностроении получила эвольвента окружности, которая:

а) позволяет сравнительно просто и точно получить профиль зуба в процессе нарезания;

б) без нарушения правильности зацепления допускает некоторое изменение межосевого расстояния a_w (это изменение может возникнуть в результате неточностей изготовления и сборки).

Эвольвентой окружности называют кривую, которую описывает точка S прямой NN, перекатываемой без скольжения по окружности радиуса г_b. Эта окружность называется эволютой или основной окружностью, а перекатываемая прямая NN — производящей прямой.

Характер эвольвентного зубчатого зацепления определяется свойствами эвольвенты.

1. Производящая прямая NN является одновременно касательной к основной окружности и нормалью ко всем производимым ею эвольвентам.

2. Две эвольвенты одной и той же основной окружности эквидистантны.

3. С увеличением радиуса r_b основной окружности эвольвента становится более пологой и при r_b > ? обращается в прямую.

4. Радиус кривизны эвольвенты в точке S₂ равен длине дуги S0B основной окружности. Центр кривизны эвольвенты в данной точке находится на основной окружности.