Геометрия зубчатых колес

Поверхности взаимодействующих зубьев должны обеспечивать постоянство передаточного числа. Основная теорема зацепления: общая нормаль, проведенная через точку касания профилей, делит расстояние между центрами зубчатых колес на части, обратно пропорциональные угловым скоростям (рис. 6.2). Все геометрические параметры зубчатых колес стандартизованы. В прямозубой передаче зубья входят в зацепление сразу по всей длине. Это явление сопровождается ударами и шумом, сила которых возрастает с увеличением окружной скорости колёс. Как правило, применяется в открытом и реже в закрытом исполнении.

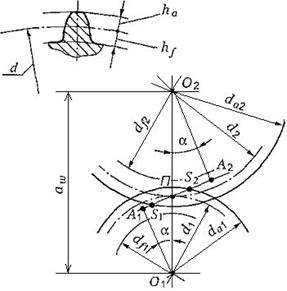
Рис. 6.2 Геометрические параметры зубчатых колес

П – полюс зацепления; А₁, А₂ - линия зацепления, S1, S2 – длина активной линии зацепления; 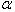- угол зацепления; 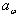- межосевое расстояние; d₁, d₂ - диаметры делительных окружностей; 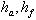- высота головки и ножки зуба; 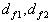- диаметры окружностей впадин, 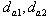- диаметры окружностей выступов. Основной параметр зубчатых колес – модуль m. Модуль равен отношению окружного шага зубьев p_t по делительной окружности к числу :

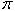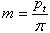(6.4)

Делительная окружность делит зуб на две части: головку и ножку. Передаточное отношение 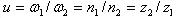(6.5)

Значение u ограничивается габаритами передачи. По СТ СЭВ 229-75 значения u (1 ряд) 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3 и т.д. Для одноступенчатых стандартных редукторов не рекомендуется принимать u>5,0.

Основные геометрические размеры определяют в зависимости от модуля m числа зубьев z:

Делительная окружность - d, начальная окружность – d_w

Диаметры делительный и начальный

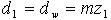(6.6)

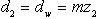(6.7)

В соответствии с параметрами исходного контура зубчатой рейки получим диаметры вершин d_a и впадин d_f зубьев:

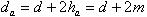(6.8)

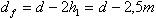(6.9)

Межосевое расстояние передачи:

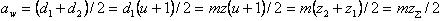
(6.10)

Здесь 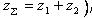- суммарное число зубьев. 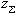Зная определяют число зубьев шестерни 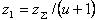и колёса 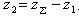. Значение z₁ округляют в ближайшую сторону до целого числа. Для прямозубых колёс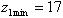

Значения межосевого расстояния 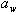, мм, выбирают из ряда чисел: 40, 50, 63, 80, 125, 140, 160, 180, 200, 224, 250, 280, 315, 355, 400, 450, 500, …, 2500 (СТ СЭВ – 75).

Из формулы (6.6) находим

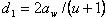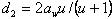; (6.11)

Ширина зубчатого венца колеса

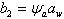(6.12)

где 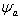- коэффициент ширины венца колеса. Ширина венца шестерни при твёрдости рабочих поверхностей зубьев менее 350 НВ:

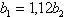(6.13).

Значения b₁ и b₂ принимают из ряда чисел R_a40. Более широкая шестерня учитывает возможное осевое смещение зубчатых колёс из-за неточности сборки, кроме того, это важно при приработке зубьев, когда более твёрдая шестерня перекрывает по ширине более мягкое колесо. При твёрдости рабочих поверхностей зубьев обоих колёс более 350 НВ принимают b₁ и b₂ (колёса не прирабатываются).