Графическое представление метода для несвязанных выборок
На Рис. 7.2 показана кривая изменения объема воспроизведения слов при разной скорости их предъявления (см. Пример). Метод дисперсионного анализа позволяет определить, что перевешивает - тенденция, выраженная этой кривой, или вариативность признака внутри групп, которая на графике схематически изображена в виде диапазонов изменения признака от минимального значения к максимальному значению в каждой группе.
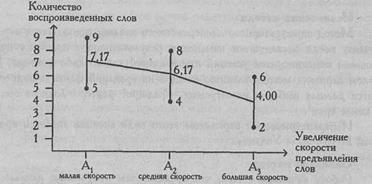
Рис. 7.2. Кривая изменения объема воспроизведения при повышении скорости предъявления слов; по каждому условию показаны диапазоны изменения признака (по данным Greene J., D'Olivera M., 1989)
Ограничения метода однофакторного дисперсионного анализа для несвязанных выборок
1. Однофакторный дисперсионный анализ требует не менее трех градаций фактора и не менее двух испытуемых в каждой градации.
2. Должно соблюдаться правило равенства дисперсий в каждой ячейке дисперсионного комплекса. Условие равенства дисперсий выполняется при использовании предлагаемой схемы расчета за счет выравнивания
количества наблюдений в каждом из условий (градаций). Правомерность этого методического приема была обоснована Г.Шеффе (1980).
3. Результативный признак должен быть нормально распределен в исследуемой выборке.
Правда, обычно не указывается, идет ли речь о распределении I признака во всей обследованной выборке или в той ее части, которая [составляет дисперсионный комплекс.
Характерно, что зарубежные руководства, в общем ссылаясь на необходимость нормального распределения данных для дисперсионного анализа, при рассмотрении конкретных схем и примеров к этому вопросу уже не возвращаются и никаких данных о распределении признака в выборке в целом или в той ее части, которая составляет дисперсионный комплекс, не приводят (см; McCall R., 1970; Welkowitz J., Ewen R.B., | Cohen J., 1982; Greene J., D'Olivera M., 1989).
Рассмотрим схему дисперсионного однофакторного анализа для несвязанных выборок, предлагаемую в руководстве J.Greene, M.D'Olivera (1989) с использованием примера этих авторов.
Пример
Три различные группы из шести испытуемых получили списки из десяти слов. Первой группе слова предъявлялись с низкой скоростью -1 слово в 5 секунд, второй группе со средней скоростью - 1 слово в 2 секунды, и третьей группе с большой скоростью - 1 слово в секунду. Было предсказано, что показатели воспроизведения будут зависеть от скорости предъявления слов. Результаты представлены в Табл. 7.2.
Таблица 7.2 Количество воспроизведенных слов (по: J.Greene, M.D'Olivera, 1989,p.99)
| № испытуемого | Группа 1: низкая скорость | Группа 2: средняя скорость | Группа 3: высокая скорость |
| Суммы | |||
| Средние | 7,17 | 6,17 | 4,00 |
| Общая сумма |
Поскольку сопоставляются разные группы, любые различия в показателях между разными условиями предъявления слов - это в то же время различия между группами испытуемых. Однако всякие различия между испытуемыми внутри каждой группы объясняются какими-то Другими, не относящимися к делу переменными, будь то индивидуальные различия между отдельными испытуемыми или неконтролируемые факторы, заставляющие их реагировать различным образом. Критерий F позволяет проверить гипотезы:
H0: Различия в объеме воспроизведения слов между группами являются не более выраженными, чем случайные различия внутри каждой группы.
H1:Различия в объеме воспроизведения слов между группами являются более выраженными, чем случайные различия внутри каждой группы. Используя экспериментальные значения, представленные в Табл. 7.2, установим некоторые величины, которые будут необходимы для расчета критерия F.
Таблица 7.3 Расчет основных величин для однофакторного дисперсионного анализа

Отметим разницу между ∑(хi2), в которой все индивидуальные значения сначала возводятся в квадрат, а потом суммируются, и (∑хi) 2где индивидуальные значения сначала суммируются для получения об- j щей суммы, а потом уже эта сумма возводится в квадрат.
Последовательность расчетов представлена в Табл. 7.4.
Часто встречающееся в этой и последующих таблицах обозначение SS - сокращение от "суммы квадратов" (sum of squares). Это сокращение чаще всего используется в переводных источниках (см., например: Гласе Дж., Стенли Дж., 1976).
SSфакт означает вариативность признака, обусловленную действием исследуемого фактора; SSобщ - общую вариативность признака; SSCA -вариативность, обусловленную неучтенными факторами, "случайную" или "остаточную" вариативность.
MS - "средний квадрат", или математическое ожидание суммы квадратов, усредненная величина соответствующих SS.
df - число степеней свободы, которое при рассмотрении непараметрических критериев мы обозначили греческой буквой v.
Таблица 7.4
Последовательность операций в однофакторном дисперсионном анализе для несвязанных выборок
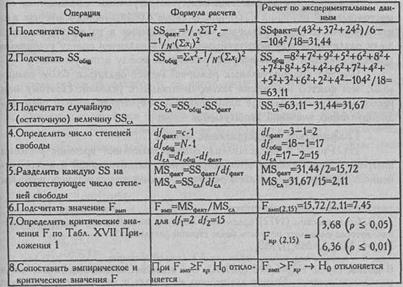
Вывод: H0 отклоняется. Принимается H1. Различия в объеме [воспроизведения слов между группами являются более выраженными, [чем случайные различия внутри каждой группы (р<0,01). Итак, скорость предъявления слов влияет на объем их воспроизведения5. Вернемся к графику на Рис. 7.2. Мы видим, что, скорее всего, значимость различий объясняется тем, что показатель воспроизведения при самой высокой скорости предъявления слов (условие 3) гораздо ниже соответствующих показателей при средней и низкой скорости.
Дата добавления: 2016-06-05; просмотров: 2124;











