ГЛАВА 8 ДИСПЕРСИОННЫЙ ДВУХФАКТОРНЫЙ АНАЛИЗ
Обоснование задачи по оценке взаимодействия двух факторов
Двухфакторный дисперсионный анализ позволяет нам оценить не только влияние каждого из факторов в отдельности, но и их взаимодействие. Может оказаться, что одна переменная значимо действует на исследуемый признак только при малых (или, напротив, больших) значениях другой переменной. Например, повышение вознаграждения может повышать скорость решения задач у высокоинтеллектуальных испытуемых и понижать ее у низкоинтеллектуальных. Усиление наказания может снижать количество агрессивных реакций у девочек и повышать его у мальчиков. Или, скажем, внушение может влиять на младших школьников, но не влиять на подростков. Один фактор может "заморозить" или, напротив, "катализировать" действие другого.
В исследовании К.А. Harris и К.В. Morrow изучалась такая личностная черта, как доминантность взрослых мужчин и женщин: Авторы предполагали, что доминантность должна быть выше у людей, которые были первенцами в своих семьях, и ниже у средних и тем более младших детей. Оказалось, что влияние каждого из двух исследуемых факторов - пола и порядка рождения - незначимо, а взаимодействие факторов значимо (см. Рис. 8.1). У мужчин доминантность, как и предполагалось, с увеличением порядка рождения снижается, а у женщин, напротив, повышается. Авторы объясняют это двояко: тем, что младшие девочки в семьях могут пользоваться особым предпочтением остальных членов семьи или тем, что повышенной доминантностью они отвечают на свое подчиненное положение в детстве (Harris K.A., Morrow K.B.,g 1992).
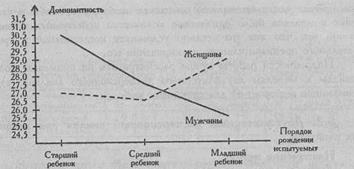
Рис. 3.1. Изменения показателей Доминантности (шкала Калифорнийского личностного опросника) в зависимости от порядка рождения у мужчин (сплошная линия) и женщин (пунктирная линия) (по: Harris А. К., Morrow К. В., 1992, р. 115)
Если нами установлено значимое взаимодействие факторов, то это зачастую важнее, чем действие каждого из факторов в отдельности. Некоторые исследователи предлагают вообще игнорировать в таких случаях "основные эффекты" каждого из взаимодействующих факторов и рассматривать только взаимодействие (McCall R., 1970, р. 250).
Специалист по возрастной и дифференциальной психологии знает, что "основных эффектов", или общих закономерностей, в действительности достаточно мало. Почти всегда требуется поправка на возраст испытуемых, их пол, профессиональную принадлежность, способ восприятия, тип энергетической мобилизации и т.п. К счастью, петербургская-ленинградская школа психологии благодаря, в первую очередь, Б.Г., Ананьеву, никогда не была "бесполой" или "вневозрастной" (см., например, Ананьев Б.Г., 1968). Именно поэтому дисперсионный анализ в большей степени отвечает ленинградскому дифференциально-психологическому подходу в экспериментальных исследованиях. Он помогает нам выявлять все более и более частные и точные закономерности и приближает нас к установлению закономерностей индивидуальных стилей.
Двухфакторный дисперсионный анализ предъявляет особые требования к формированию комплексов. Комплекс должен представлять собой симметричную систему: каждой градации фактора А должно соответствовать одинаковое количество градаций фактора В. Например, для исследования А.К. Harris, К.В. Morrow (см. Рис. 8.1) это означает, что и среди мужчин должны были быть старшие, средние и младшие дети, и среди женщин должны быть старшие, средние и младшие дети, причем для равномерного комплекса необходимо, чтобы в каждой ячейке комплекса было одинаковое количество испытуемых. Понятно, конечно же, что это значительно усложняет исследование и требует тщательного предварительного планирования его.
Подробности работы лучше рассматривать на примерах, поэтому перейдем к моделям двухфакторного дисперсионного анализа: а) для несвязанных выборок; б) для связанных выборок.
8.2. Двухфакторный дисперсионный анализ для несвязанных выборок
Назначение метода
Данный вариант двухфакторного дисперсионного анализа применяется в тех случаях, когда исследуется одновременное действие двух факторов на разные выборки испытуемых, т. е. когда разные выборки, испытуемых оказываются под воздействием разных сочетаний двух факторов. Количество выборок определяется количеством ячеек дисперсионного комплекса.
Описание метода
Суть метода остается прежней, но в двухфакторном дисперсионном анализе мы можем проверить большее количество гипотез. Расчеты гораздо сложнее, чем в однофакторных комплексах.
Используемый в данном руководстве алгоритм расчетов предназначен только для равномерных комплексов. Если комплекс получился неравномерным, необходимо случайным образом отсеять несколько испытуемых.
Работу начинаем с построения специальной таблицы, отражающей весь дисперсионный комплекс. Подробности лучше сразу рассматривать на примере.
Пример
Рассмотрим пример из руководства J.Greene, M.D.'Olivera (1989).
Четырем группам испытуемых предъявлялись списки из 10 слов:
группе 1 - короткие слова с большой скоростью;
группе 2 - короткие слова с медленной скоростью;
группе 3 - длинные слова с большой скоростью;
группе 4 - длинные слова с медленной скоростью.
В каждой группе было по 4 испытуемых, всего N=16. Предсказывалось, что между факторами длины слов и скоростью их предъявления будет наблюдаться значимое взаимодействие: при большой скорости предъявления лучше будут запоминаться короткие слова, а при медленной скорости - длинные слова. Результаты экспериментов представлены в Табл. 8.1.
Таблица 8.1
Количество воспроизведенных слов при разной длине слов и разной скорости их предъявления (по J.Greene, M.D'Olivera, 1989)
| Переменная (фактор) В скорость предъявления слов | Переменная (фактор) А - длина слов | Суммы по переменной В (ТB) | |||
| A1 - короткие слова | A2 - длинные слова | ||||
| В1 (большая скорость) | |||||
| B2(малая скорость) | |||||
| Суммы по переменной А (ТA) |
Заметим, что в отечественных руководствах чаще предлагается другая, более привычная для нас, форма таблиц для двухфакторных дисперсионных комплексов (Табл. 8.2). При такой форме легче "увидеть" комплекс в целом.
Таблица 8.2
Двухфакторный дисперсионный комплекс по оценке влияния фактора А (длина слов) и фактора В (скорость предъявления слов) на количество воспроизведенных слов
| Градации фактора А | А1 - короткие слова | A2 – длинные слова | ||
| Градации фактора В | B1 | B2 | B1 | B2 |
| Суммы по ячейкам | ||||
| Суммы по градациям фактора А | ТA1=45 | ТA2=40. | ||
| Суммы по градациям фактора В | ТB1==30+15=45 | ТB2==15+25=40 |
Как видим, при такой форме таблицы легче подсчитать суммы по ячейкам (в столбик), но труднее разобраться с суммами по градациям каждого из факторов. В данном случае оказалось, что они совпали:
ТA1= ТB1; ТA2= ТB2.
В дальнейшем при использовании алгоритма расчетов будем опираться на Табл. 8.1.
Сформулируем гипотезы. Это будут гипотезы, касающиеся влияния фактора А отдельно от фактора В (как бы при "усредненных" его значениях), гипотезы о влиянии фактора В отдельно от фактора А игипотезы о влиянии взаимодействия градаций факторов А и В.
1 комплект гипотез
H0: Различия в объеме воспроизведения слов, обусловленные действием фактора А, являются не более выраженными, чем случайные различия между показателями.
H1: Различия в объеме воспроизведения слов, обусловленные действием фактора А, являются более выраженными, чем случайные различия между показателями.
2 комплект гипотез
H0: Различия в объеме воспроизведения слов, обусловленные действием фактора В, являются не более выраженными, чем случайные различия между показателями.
H1: Различия в объеме воспроизведения слов, обусловленные действием фактора В, являются более выраженными, чем случайные различия между показателями.
3 комплект гипотез
H0: Влияние фактора А на объем воспроизведения слов одинаково при разных градациях фактора В, и наоборот.
H1:Влияние фактора А на объем воспроизведения слов различно при разных градациях фактора В, и наоборот.
Используя экспериментальные значения, представленные в Табл. 8.1, установим некоторые величины, которые будут необходимы для расчета критериев F.
Таблица 8.3
Величины, необходимые для расчета критериев F в двухфакторном дисперсионном анализе для несвязанных выборок

Напомним, что при подсчете ∑ x i2 все индивидуальные значения сначала возводятся в квадрат, а потом суммируются, а при подсчете (∑ x i)2 все индивидуальные значения сначала суммируются, а затем их общая сумма возводится в квадрат.
Последовательность расчетов представлена в Табл. 8.4.
Таблица 8.4
Последовательность операций в двухфакторном дисперсионном анализе для несвязанных выборок
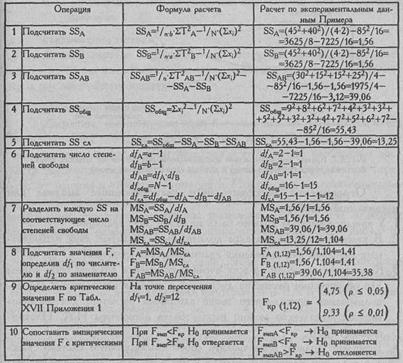
Вывод: Но принимается в комплектах гипотез 1 и 2. Различия в объеме воспроизведения слов, обусловленные в отдельности факторами А и В, не являются более выраженными, чем случайные различия между показателями. H0 отвергается для взаимодействия факторов (3 комплект). Принимается H1. Влияние фактора А на объем воспроизведения слов различно при разных градациях фактора В, и наоборот (р≤0,01).
Итак, оказывается, что факторы длины слов и скорости их предъявления в отдельности не оказывают значимого действия на объем воспроизведения. Значимым оказывается именно взаимодействие факторов: короткие слова лучше запоминаются при быстрой скорости предъявления, а длинные - при медленной скорости предъявления (см. Рис. 8.2). Таким образом, предположение, высказанное авторами, нашло статистически значимое подтверждение (р≤0,001).
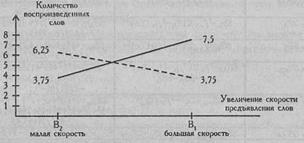
Рис. 8.2. Кривые изменения объема воспроизведения при повышении скорости предъявления коротких (сплошная линия) и длинных слов (пунктирная линия)
Дата добавления: 2016-06-05; просмотров: 3199;











