Проверка нормальности распределения результативного признака.
Дисперсионный анализ относится к группе параметрических методов и поэтому его следует применять только тогда, когда известно илидоказано, что распределение признака является нормальным (Суходольский Г.В., 1972; Шеффе Г., 1980 и др.). Строго говоря, перед тем, как применять дисперсионный анализ, мы должны убедиться в нормальности распределения результативного признака. Нормальность распределения результативного признака можно проверить путем расчета показателей асимметрии и эксцесса и сопоставления их с критическими значениями (Пустыльник Е.И., 1968* Плохинский Н.А., 1970 и др.).
Произведем необходимые расчеты на примере параграфа 8.3, в котором анализируется длительность мышечного волевого усилия.
Действовать будем по следующему алгоритму:
а) определим показатели асимметрии и эксцесса по формулам Н.А. Плохинского и сопоставим их с критическими значениями, указанными Н.А. Плохинским;
б) рассчитаем критические значения показателей асимметрии и эксцесса по формулам Е.И. Пустыльника и сопоставим с ними эмпирические значения;
в) если эмпирические значения показателей окажутся ниже критических, сделаем вывод о том, что распределение признака не отличается от нормального.
Таблица 7.1
Вычисление показателей асимметрии и эксцесса по показателю длительности попыток решения анаграмм
| № | хi | (хi – 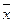 ) )
| (хi – 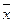 )2 )2
| (хi – 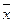 )3 )3
| (хi – 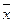 )4 )4
|
| 0,94 | 0,884 | 0.831 | 0,781 | ||
| 2,94 | 8,644 | 25,412 | 74,712 | ||
| 1.94 | 3,764 | 7,301 | 14,165 | ||
| -1,06 | 1,124 | -1,191 | 1,262 | ||
| -0.06 | 0,004 | -0,000 | 0,000 | ||
| 0,94 | 0,884 | 0,831 | 0,781 | ||
| -2,06 | 4,244 | -8.742 | 18,009 | ||
| -0,06 | 0,004 | -0,000 | 0,000 | ||
| 4,94 | 24,404 | 120,554 | 595,536 | ||
| 3,94 | 15,524 | 61,163 | 240,982 | ||
| И | -2,06 | 4,244 | -8,742 | 18,009 | |
| -3.06 | 9,364 | -28,653 | 87,677 | ||
| -0.06 | 0,004 | -0,000 | 0,000 | ||
| -0,06 | 0.004 | -0,000 | 0,000 | ||
| -5,06 | 25,604 | -129,554 | 655,544 | ||
| -2,06 | 4,244 | -8,742 | 18,009 | ||
| Суммы | 102,944 | 30,468 | 1725,467 |
Для расчетов в Табл. 7.1 необходимо сначала определить среднюю арифметическую по формуле:
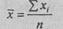
где хi - каждое наблюдаемое значение признака;
n - количество наблюдений. В данном случае:
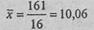
Стандартное отклонение (сигма) вычисляется по формуле:
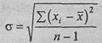
где хi - каждое наблюдаемое значение признака; 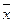 – среднее значение (среднее арифметическое); n - количество наблюдений. В данном случае:
– среднее значение (среднее арифметическое); n - количество наблюдений. В данном случае:
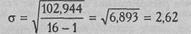
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:
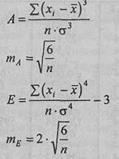
где (хi –  ) - центральные отклонения;
) - центральные отклонения;
σ - стандартное отклонение;
п - количество испытуемых. В данном случае:
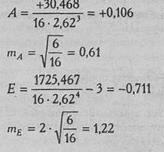
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
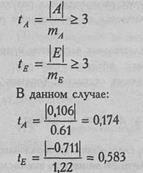
Мы видим, что оба показателя не превышают в три раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального.
Теперь произведем проверку по формулам Е.И. Пустыльника. Рассчитаем критические значения для показателей А и Е:
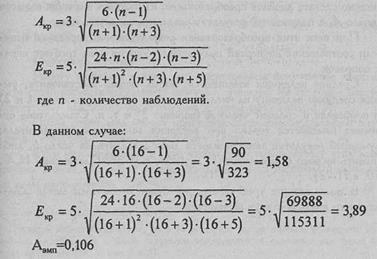
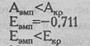
Итак, оба варианта проверки, по Н.А. Плохинскому и по Е.И. Пустыльнику, дают один и тот же результат: распределение результативного признака в данном примере не отличается от нормального распределения.
Можно выбрать любой из двух предложенных вариантов проверки и придерживаться его. При больших объемах выборки, по-видимому, стоит производить расчет первичных статистик (оценок параметров) на ЭВМ.
Дата добавления: 2016-06-05; просмотров: 3412;











