Случай 3. Другие критерии слишком трудоемки
Этот случай чаще всего относится к критерию χ2. Заменить его критерием φ* можно при условии, если сравниваются распределения признака в двух выборках, а сам признак принимает всего два значения[24].
В качестве примера можно привести задачу с соотношением мужских и женских имен в записных книжках двух психологов (см. п. 4.2, Табл. 4.11).
Преобразуем Табл. 4.11 в четырехклеточную таблицу, где "эффектом" будем считать мужские имена.
Таблица 5.18
Четырехклеточная таблица для подсчета φ* при сопоставлении записных книжек двух психологов по соотношению мужских и женских имен
| Группы | "Есть аффект": мужские имена | "Нет аффекта»: женские имена | Суммы | ||
| Группа 1 - выборка имен в книжке X. | (32,8%) | (67,2%) | |||
| Группа 2 - выборка имен в книжке С. | (35,1%) | (64,9%) | |||
| Суммы |
Сформулируем гипотезы.
H0: Доля мужских имен в записной книжке С. не больше, чем в записной книжке X.
H1: Доля мужских имен в записной книжке С. больше, чем в записной книжке X.
Далее действуем по алгоритму.

По Табл. XIII Приложения 1 определяем, какому уровню достоверности соответствует это значение. Мы видим, что такого значения вообще нет в таблице. Построим "ось значимости".
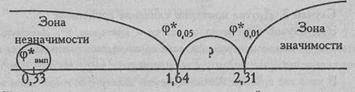
Полученное эмпирическое значение - далеко в "зоне незначимости".
f*эмп>f*теор
Ответ: H0 принимается. Доля мужских имен в записной книжке психолога С. не больше, чем в запиской книжке психолога X.
Исследователь сам может решить для себя, какой метод ему в данном случае удобнее применить - χ2 или φ*. Похоже, что во втором случае меньше расчетов, хотя чуда не произошло: различия по-прежнему недостоверны.
Итак, мы убедились, что критерий φ* Фишера может эффективно заменять традиционные критерии в тех случаях, когда их применение невозможно, неэффективно или неудобно по каким-то причинам.
Биномиальный критерий m может служить заменой критерия χ2 в случае альтернативных распределений или в случае, когда признак может принимать одно из нескольких значений и вероятность того, что он примет определенное значение, известна.
В качестве примера можно привести исследование, посвященное распределению предпочтений по 4-м типам мужественности (см. Задачу 3 к Главе 4). Если бы для испытуемых все 4 типа мужественности были одинаково привлекательными, то на первом месте примерно одинаковое количество раз оказывался бы каждый из типов. Иными словами, вероятность оказаться на первом месте для каждого типа составляла бы 1/4 т.е. Р=0.25.
В действительности же Национальный тип оказался на 1-м месте 19 раз, Современный - 7 раз, Религиозный - 3 раза и Мифологический - 2 раза. Можно попытаться определить, достоверно ли Национальный тип чаще оказывается на 1-м месте, чем это предписывается вероятностью Р=0,25?
Сформулируем гипотезы.
H0; Частота попадания Национального типа мужественности на 1-е место в ряду предпочтений не превышает частоты, соответствующей вероятности Р=0,25.
H1: Частота попадания Национального типа мужественности на 1-е место в ряду предпочтений превышает частоту, соответствующую вероятности Р=0,25.
Определим теоретическую частоту попадания того или иного типа мужественности на 1-е место при равновероятном выборе:
fтеор=n·Р=31-0,25=7,75
В данном случае соблюдаются требования, предусмотренные ограничением 3: Р=0,25<0,50; fэмп>fтеор. Мы можем использовать биномиальный критерий при n<50. В данном случае n=31. По Табл. XV Приложения 1 определяем критические значения m при n=31, Р=0,25; Q=0,75:
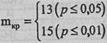
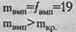
Ответ: H0 отвергается. Частота попадания Национального типа мужественности на 1-е место в ряду предпочтений превышает частоту, соответствующую вероятности Р=0,25 (р<0,01).
Итак, Национальный тип мужественности действительно чаще оказывается на 1-м месте, чем это происходило бы в том случае, если бы он выбирался на 1-е место равновероятно с другими типами.
Отметим, что мы проверяли гипотезу не об отличии данного типа мужественности от других типов, а об отличии частоты его встречаемости от теоретически возможной величины при равновероятном выборе. Все остальные типы и остальные позиции выбора остаются "за кадром" нашего рассмотрения.
Аналогичным образом можно сопоставить с теоретической частотой эмпирическую частоту попадания любого другого типа на любую другую позицию.
Дата добавления: 2016-06-05; просмотров: 1714;











