Ограничения критерия Пейджа
1. Нижний порог - 2 испытуемых, каждый из которых прошел не менее 3-х замеров в разных условиях. Верхний порог - 12 испытуемых и 6 условий (n≤12, c≤6). Критические значения критерия L даны по руководству J.Greene, M. D'Olivera (1989). Они предусматривают три уровня статистической значимости: р≤0,05; р≤0,01; р≤0,001.
2. Необходимым условием применения теста является упорядоченность столбцов данных: слева должен располагаться столбец с наименьшей ранговой суммой показателей, справа - с наибольшей. Можно просто пронумеровать заново все столбцы, а потом вести расчеты не слева направо, а по номерам, но так легче запутаться.
Пример
Продолжим рассмотрение примера с анаграммами. В Табл. 3.7 показатели времени решения анаграмм и их ранги представлены уже в упорядоченной последовательности: анаграмма 1, анаграмма 3, анаграмма 2. Действительно ли время решения увеличивается при такой последовательности предъявления анаграмм?
Таблица 3.7
Показатели времени решения анаграмм 1, 3, 2 и их ранги (n=5)
| Код имени испытуемого | Условие 1: Анаграмма 1 | Условие 2: Анаграмма 3 | Условие 3: Анаграмма 2 | ||||
| Время (сек) | Ранг | Время (сек) | Ранг | Время (сек) | Ранг | ||
| Л-в | |||||||
| П-о | |||||||
| К-в | |||||||
| Ю-ч | |||||||
| Р-о | |||||||
| Суммы | |||||||
| Средние | 10,2 | 9,4 |
Сумма рангов составляет: 6+9+5=30. Расчетная сумма:
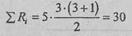
Реально полученная и расчетная суммы совпадают, мы можем двигаться дальше.
Как видно из Табл. 3.7, среднее время решения анаграммы 3 даже меньше, чем анаграммы 1. Однако мы исследуем не среднегруп-повые тенденции, а степень совпадения индивидуальных тенденций. Нам важен именно порядок, а не абсолютные показатели времени. Поэтому и формулируемые нами гипотезы - это гипотезы о тенденциях изменения индивидуальных показателей.
Сформулируем гипотезы.
Н0: Тенденция увеличения индивидуальных показателей от первого условия к третьему является случайной.
H1: Тенденция увеличения индивидуальных показателей от первого условия к третьему не является случайной. Эмпирическое значение L определяется по формуле:
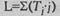
где Ti- сумма рангов по каждому условию;
j - порядковый номер, приписанный каждому условию в новой последовательности .
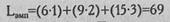
По Табл. VIII Приложения 1 определяем критические значения L для данного количества испытуемых: n=5, и данного количества условий: с=3.
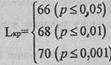
Построим "ось значимости"
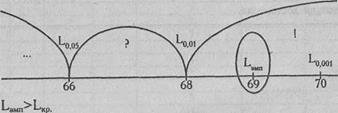
Ответ: Н0 отклоняется. Принимается H1. Тенденция увеличения индивидуальных показателей от первого условия к третьему не является случайной (р<0,01). Последовательность анаграмм: 1(КРУА), З(ИНААМШ), 2(АЛСТЬ), - будет в большей степени отвечать замыслу экспериментатора о постепенном возрастании сложности задач, чем первоначально применявшаяся последовательность.
АЛГОРИТМ 11
Дата добавления: 2016-06-05; просмотров: 2113;











